Proving the Worst Case Time Complexity for Computing a "Binary Decision Diagram"
Solving decades-old unsolved problems in computer science

News Highlights:

Background

A binary decision diagram is a data structure that represents a family of sets. A family of sets is a set whose elements are sets. For example, {{1, 2}, {2, 3}} is a family of sets made up of two sets {1, 2} and {2, 3}. Various objects can be represented as a family of sets, such as logical circuits, travel paths from one point to another, and combinations of coupons that can be used simultaneously. Because of the versatility of set families and their convenience as data structures, binary decision diagrams have been used in various problems involving set families, such as circuit design, communication network analysis, and AI. For example, in communication network analysis, it has been found that the analysis time can be significantly reduced by representing the communication patterns of a network with multiple points connected as a family of sets, and then expressing them using a binary decision diagram (Figure 1).⁴

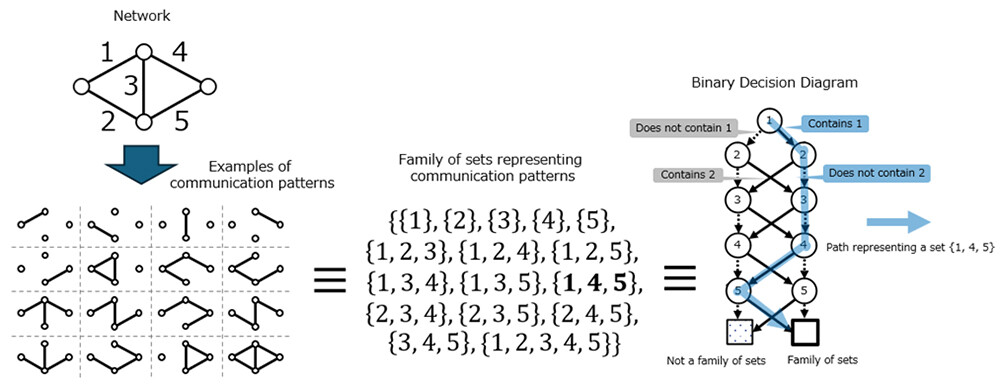Figure 1 An Example of A Family of Sets and Binary Decision Diagram That Represent Network Communication Patterns Note. In the figure, 16 communication patterns are represented by a family of sets of 16 sets, which are compressed into a binary decision diagram of 11 nodes.
(Left) Diagram of a network connecting four points and an example of 16 communication patterns.
(Middle) Communication patterns are represented by a family of sets, where the elements are the numbers of each edge.
(Right) A binary decision diagram where each node represents the decision regarding an element's inclusion in a set in the family of sets. Every set in a family is represented as a downward path from the top to the bottom (T) through the nodes. In a path corresponding to a set, a solid line indicates that the corresponding element is included in the set, and a dotted line indicates that the element is not included. The blue path proceeds from 1 to 2 via a solid line, from 2 to 3 via a dotted line, and from ..., 5 to T by a solid line, so that the set {1, 4, 5} is included in the family of sets.

An important feature of binary decision diagrams is that a binary decision diagram representing one family of sets can be efficiently constructed by applying various operations (referred to as operations on a binary decision diagram) to another diagram representing different family of sets (Figure 2). For example, given two binary decision diagrams, we can efficiently construct a binary decision diagram representing the union of their families or the join of their families. By using these operations, one can flexibly perform a variety of operations on the family of sets, such as extracting a set of paths with a travel distance less than or equal to a certain value. Various operations have been developed and applied in the field of binary decision diagram research.

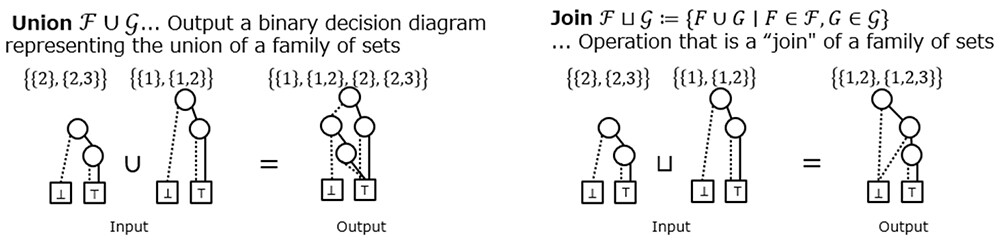Figure 2 Example of Binary Operations on a Binary Decision Diagram Note. Two binary decision diagrams representing a family of sets are received as inputs, and a binary decision diagram representing a result of performing an operation on them is output.

However, the worst-case time complexity for operations on binary decision diagrams was not well understood for many operations except for basic ones. Furthermore, although some operations are described in popular textbooks as executable in polynomial time, there has been no proof to confirm that they are executable in polynomial time.

Details of the results

In this study, we theoretically show for the first time that the execution of a major set of operations on binary decision diagrams, whose computational complexity was previously unknown, may take an exponential time with respect to the input size in the worst case. Specifically, given the number of variables n, the worst-case complexity was established by analyzing scenarios where the binary decision diagram of the input is on the order of a polynomial with respect to n, but the size of the output grows exponentially for several cases. Some operations are widely used, but their complexity has remained unknown for decades. Therefore, this study resolves long-standing unsolved problems related to binary decision diagrams.

Point of the technology

It has long been known that the size of the decision diagram increases exponentially when the intersection and union operations, which are fundamental operations of binary decision diagrams. However, this study discovered that a single operation can replace multiple repeated intersection and union operations for cases where complexity was previously unknown, such as the product of set families (Join). Based on this finding, we proved that it is impossible to perform operations in polynomial time by demonstrating an example where the size of a binary decision diagram increases exponentially with just a single operation (Figure 3).

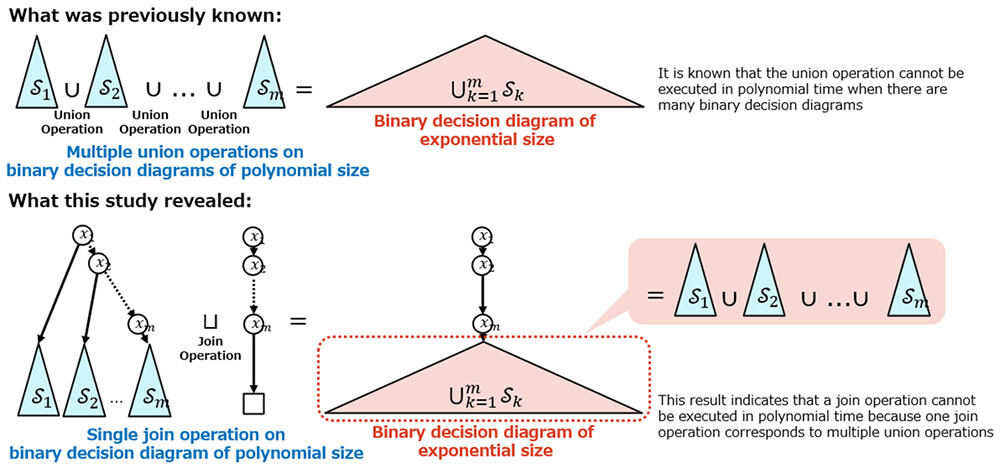Figure 3 Proof that A Join Operation on Binary Decision Diagrams Is Infeasible in Polynomial Time

Significance of research and future development

This research clarified the worst-case computation times for all major operations on binary decision diagrams. It represents a highly influential theoretical work that can be applied to problem-solving using binary decision diagrams, a widely used data structure. By clarifying the computational complexity, it is possible to make decisions such as avoiding the use of certain operations to prevent exponential growth in computational complexity, contributing to the design of more efficient algorithms. In the TAOCP, a well-known textbook on computer science, there was a description indicating that some operations, which are revealed by this study to actually take exponential time, could be computed in polynomial time. This finding points out an error in that description, and the team's revised proposal has been accepted by the author, Dr. Donald Knuth, and will be reflected in the revised edition of TAOCP.

[Paper Information]

Conference: 35th International Symposium on Algorithms and Computation (ISAAC 2024)
Title: Single Family Algebra Operation on BDDs and ZDDs Leads to Exponential Blow-Up
Author: Kengo Nakamura, Masaaki Nishino, and Shuhei Denzumi
DOI: 10.4230/LIPIcs.ISAAC.2024.52
URL: https://doi.org/10.4230/LIPIcs.ISAAC.2024.52

[Research Grants]

This study was supported by JST CREST (Grant Number: JPMJCR22D3) and JSPS KAKENHI (Grant Numbers: JP20H05963, JP23H04391).

[Glossary]

^1.Family of sets: A collection of sets. For example, {{1, 2}, {2, 3}} is a family of sets formed by collecting sets {1, 2} and {2, 3}, which are combinations of numbers. In an example of network analysis, by expressing a connection path connecting two points on a network as a set of links, a collection of a plurality of connection paths can be expressed as a family of sets.

^2.Exponential time algorithm: An algorithm whose execution time increases exponentially with n, where n is the input size of the problem to be solved.

^3.Polynomial time algorithm: An algorithm whose execution time can be upper bounded by a polynomial of n, where n is the input size of the problem to be solved.

^4.Larger scale analysis can be found here.
https://www.rd.ntt/e/research/JN202409_29259.html

About NTT

NTT contributes to a sustainable society through the power of innovation. We are a leading global technology company providing services to consumers and businesses as a mobile operator, infrastructure, networks, applications, and consulting provider. Our offerings include digital business consulting, managed application services, workplace and cloud solutions, data center and edge computing, all supported by our deep global industry expertise. We are over $93B in revenue and 330,000 employees, with $3.6B in annual R&D investments. Our operations span across 80+ countries and regions, allowing us to serve clients in over 190 of them. We serve over 75% of Fortune Global 100 companies, thousands of other enterprise and government clients and millions of consumers.