100,000-spin coherent Ising machine
～High-speed solution search for large-scale combinatorial optimization problems enabled with a large-scale optical computer～

Coherent Ising machines (CIMs) are drawing attention as a new type of computer that can solve combinatorial optimization problems using a network of degenerate optical parametric oscillators (DOPOs). Nippon Telegraph and Telephone (NTT) Corporation, in collaborative research with the National Institute of Informatics (NII), has constructed a CIM based on a network of 100,000 DOPOs--the world's largest CIM.
 As the progress of digital computers has started to show saturation recently, many institutions around the world are now pursuing research on new types of computers that can solve some specific problems using physical phenomena. A CIM has been studied by several institutions, including NTT, NII, and Stanford University, as a computer to solve combinatorial optimization problems using DOPOs. In 2016, a research team including NTT reported a large-scale CIM that solves 2,000-node optimization problems. In the CIM, 2,000 DOPO pulses were generated in a long-distance fiber cavity, and the pulses were coupled via a scheme called measurement feedback, with which all-to-all coupling among the pulses (which amounts to four million couplings) was achieved. In the present work, we significantly extended the scale of the CIM to 100,000 DOPO pulses with ten billion couplings. We demonstrated that the CIM could find an approximate solution to a 100,000-node combinatorial optimization problem 1,000 times faster than simulated annealing (SA) implemented on a CPU. We also confirmed that we can obtain a broad distribution of solutions with some very good ones. This characteristic may make the CIM useful for applications that require fast sampling such as lead optimization and machine learning.
 The paper describing this work was published in the American journal "Science Advances" on September 29 at 14:00 Eastern Standard Time (EST). This research was partially funded by the Impulsing Paradigm Change through Disruptive Technologies (ImPACT) Program of the Council of Science, Technology and Innovation (Cabinet Office, Government of Japan).

Background

Faced with the impending saturation of the progress of digital computers, researchers are intensively studying special-purpose computers based on physical phenomena. An "Ising machine" is one such computer, which simulates the Ising model using a physical system that mimics the behavior of a spin. Since a combinatorial optimization problem can be converted to a ground state search problem of the Ising model with polynomial resources, we can solve various optimization problems using Ising machines. The physical systems to simulate the Ising spins include trapped ions, single electron devices, and nanomechanical devices. In particular, remarkable progress has been made in development of a quantum annealer based on superconducting quantum bits, which can now solve Ising model problems with ~5,000 spins. Moreover, computing systems that emulate the concept of such Ising machines on digital hardware have also been reported.

A coherent Ising machine is one such computer, where the discretized phases of degenerate optical parametric oscillators (DOPOs) are used to simulate the Ising spins. In contrast to quantum annealers using superconducting quantum bits, the CIM can work at room temperature thanks to the use of high-frequency optical oscillators to mimic spins. A research team formed by NTT, NII, Osaka University, the University of Tokyo, and Stanford University reported a CIM, where 2,048 DOPO pulses were generated in a ring cavity that included a 1-km optical fiber, and the pulses were coupled using an optical-electrical hybrid scheme called measurement feedback. The team performed a benchmark experiment using a maximum cut problem of a 2,000 node graph to show that the CIM could find approximate solutions to the problem faster than simulated annealing implemented on a CPU; however, the seed-up factor was limited to ~50.
 In this work, we extended the scale of the optical system and measurement-feedback circuit to construct the world's largest Ising machine, which can simulate the Ising model with up to 100,512 spins and 10 billion couplings. Using the 100,000-spin CIM, we solved a maximum cut problem of a fully connected 100,000-node graph, and found that the CIM could find approximate solutions with a particular solution accuracy 1,000-times faster than SA implemented on a CPU. We also found that the CIM operated at near the DOPO threshold could deliver a broad solution distribution with some very good solutions compared the distribution obtained by SA.

Results

In the CIM, we turn on and off a phase-sensitive amplifier (PSA) placed in a 5-km fiber cavity with a temporal interval of 200 ps. The PSA amplifies the 0- or π-phase components of the incoming light efficiently. The weak optical noise pulses initially generated in the PSA undergo multiple phase-sensitive amplifications, and after many circulations in the cavity, eventually oscillate at the 0 or π phase to form DOPO pulses. Since the propagation time of the optical pulses in the 5-km fiber is about 25 μs, we can obtain more than 120,000 DOPO pulses multiplexed in the time domain. For every circulation in the cavity, we split off a portion of all the DOPO pulses to measure their phases and amplitudes, and the measurement results are input into a fast matrix multiplier circuit, to which we upload a 100,512 x 100,512 matrix that corresponds to a given Ising model problem in advance. The matrix multiplier circuit performs the multiplication of the matrix and measurement results (100,512-element vector) to obtain the feedback signal for each pulse in the next circulation. Then the feedback signal is used to modulate an optical pulse whose wavelength is same as that of the DOPO, and the pulse is injected to the corresponding DOPO pulse to complete the coupling. By using the optical and electrical hybrid approach, we can implement all possible combinations of two-body interactions among the 100,512 DOPO pulses, which amounts to as many as 10,102,662,144. By repeating phase-sensitive amplification and measurement feedback many times (ranging from several ten to several hundred times), the network of DOPO pulses takes a phase configuration that stabilizes the whole system. Finally, by assigning +1/-1 spin states to 0/π of DOPO phases, we can obtain fine approximate solutions to the given Ising problem.

Evaluation of computation time

Evaluation of solution accuracy

Technical features

1. Generation and stabilization of 100,000 DOPO pulses

The setup of the optical system is shown in Fig. 4. We put a periodically-poled lithium niobate (PPLN) waveguide in a 5-km fiber ring cavity. To suppress changes in the propagation time in the cavity, the 5-km fiber was placed in a temperature-controlled box, and the fiber temperature was stabilized within ±0.05℃ accuracy by using Peltier devices. The phase of the fiber ring cavity was stabilized by feedback control by using piezoelectric devices. Moreover, the use of dispersion shifted polarization maintaining fiber for the fiber ring cavity enabled stable DOPO pulse formation. We input a pump pulse train with a wavelength of 780 nm and a 5-GHz repetition frequency into the PPLN waveguide. Consequently, the PPLN worked as a PSA at the 1560-nm wavelength (doubled wavelength of the pump) to generate DOPO pulses with a 5-GHz repetition frequency.
 Compared with our previously reported CIM with a 1-km fiber ring and 1-GHz repetition pump pulses, the cavity loss increased because of the longer fiber, and the pump peak power decreased because of the higher repetition frequency in the present CIM. To overcome these issues, we needed to increase the efficiency of the PPLN waveguide. In this work, we increased the PPLN waveguide's efficiency by improving the uniformity of the refractive index of the waveguide using high-resolution photo-lithography and dry etching. The coupling efficiency between the PPLN waveguide and the fiber pigtail was also improved. As a result, we were able to increase the overall module efficiency by three times compared with the previous one.

2. Construction of large-scale matrix multiplication system

In the measurement feedback for the present CIM, we need to complete multiplication of a 100,512 x 100,512 matrix and a 100,512-element vector within 25 μs, which corresponds to the round-trip time in the 5-km fiber ring cavity. This requires a computation speed of 1,000 tera-operations per second and a memory bandwidth for matrix readout of 100 terabytes per second. To achieve this, we developed a custom-made system that parallelizes matrix calculations, which enabled the all-to-all coupling among the 100,512 DOPO pulses.

Future perspective

We plan to pursue basic research for utilizing the CIM's broad solution distributions in applications that require sampling, such as lead optimization and machine learning. We will also search for applications of LASOLV, a computation system based on the CIM concept, to large-scale combinatorial optimization.

Figures

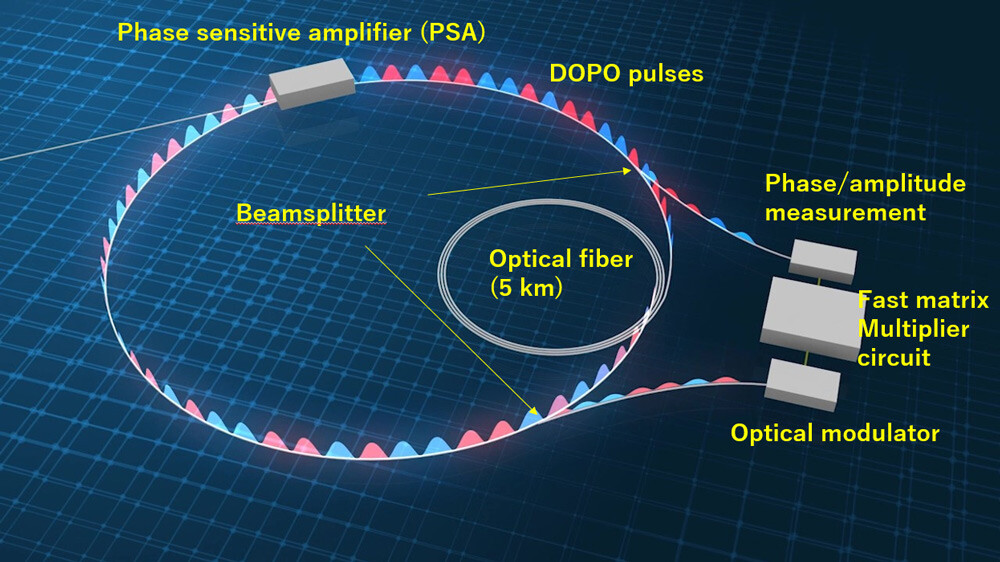Figure 1: Schematic diagram of the CIM concept. A phase sensitive amplifier (PSA) amplifies 0 or π-phase components of the incoming light in a 5-km fiber ring cavity. By turning the PSA on and off with a 200-ps temporal interval, we generate ~120,000 DOPO pulses. A portion of pulse energy is split by a beamsplitter for measuring the phases and amplitudes. To obtain a feedback signal for each DOPO pulse, the measurement results are input into a fast matrix multiplication circuit, in which a given Ising model problem (a 100,512 x 100,512 matrix) has been installed in advance. The feedback signal is used to modulate an optical pulse whose wavelength is the same as that of the DOPO pulses, and the pulse is injected into the corresponding DOPO pulse circulating in the cavity. By repeating this procedure multiple times (typically several ten to several hundred times), the DOPO network takes a phase configuration that stabilizes the whole system, which gives an approximate solution to the given Ising model problem.

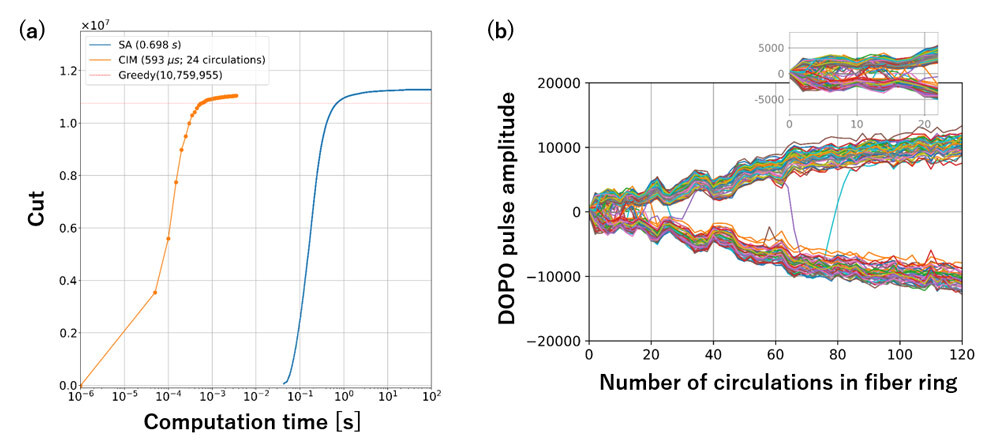Figure 2: Evaluation of computation time. (a) Temporal evolutions of cut values in solving maximum cut problem of 100,000-node complete graph obtained with the CIM and SA implemented on a CPU. The red dotted line corresponds to a reference score obtained with a Greedy algorithm. Times to reach the reference score were 0.7 s with SA and 600 μs with the CIM. (b) Temporal evolution of DOPO pulse amplitudes obtained in the CIM computation shown in (a). Trajectories of 100 pulses among 100,000 are plotted.

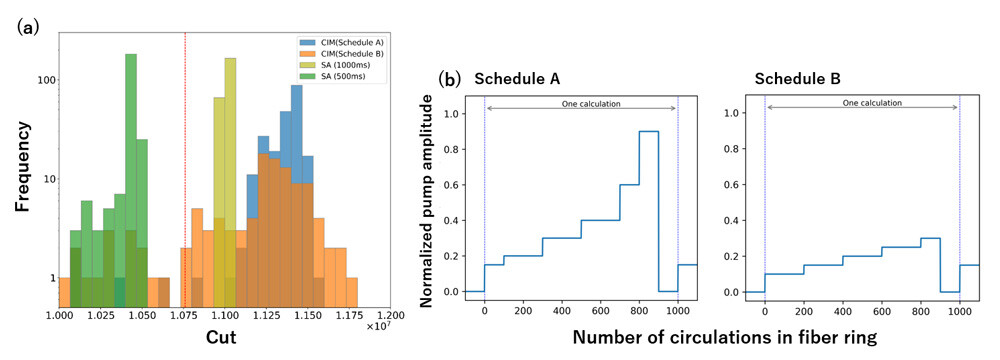Figure 3: Evaluation of solution accuracy. (a) Cut histogram obtained when solving maximum cut problem of 100,000-node complete graph many times. The computation time of the CIM was 22 ms. (b) Temporal changes of the pump amplitudes to the PPLN waveguide. In Schedule B we operate the DOPOs at near the threshold using relatively small pump amplitude.

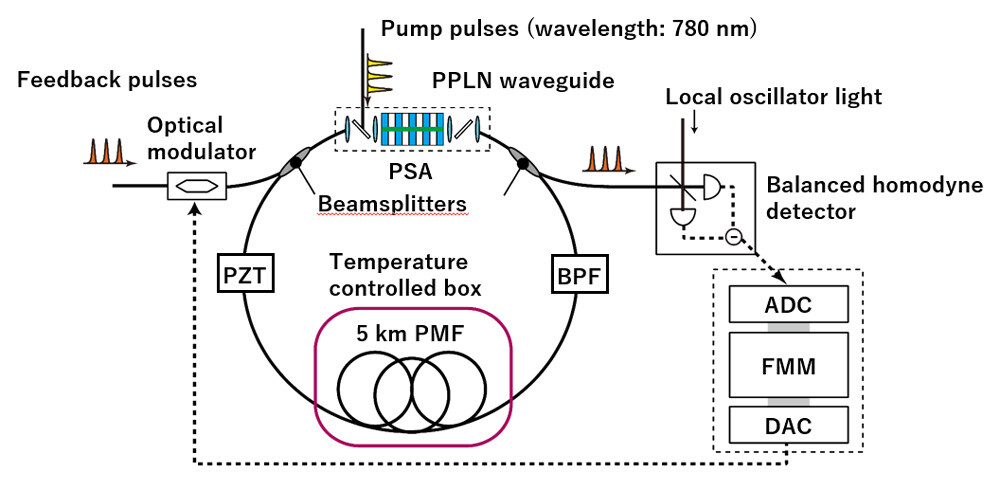Figure 4: Details of the CIM experimental setup. PZT: a fiber stretcher based on piezoelectric device. BPF: optical bandpass filter. PMF: polarization maintaining fiber. ADC: analog-to-digital converter. FMM: fast matrix multiplier circuit. DAC: digital-to-analog converter.

Figure 5: Appearance of the 100,000-spin CIM.

Publication information

Toshimori Honjo, Tomohiro Sonobe, Kensuke Inaba, Takahiro Inagaki, Takuya Ikuta, Yasuhiro Yamada, Takushi Kazama, Koji Enbutsu, Takeshi Umeki, Ryoichi Kasahara, Ken-ichi Kawarabayashi, Hiroki Takesue, "100,000-spin coherent Ising machine," Science Advances 7 (40), eabh0952 (2021).