Microsoft ends support for Internet Explorer on June 16, 2022.
We recommend using one of the browsers listed below.
- Microsoft Edge(Latest version)
- Mozilla Firefox(Latest version)
- Google Chrome(Latest version)
- Apple Safari(Latest version)
Please contact your browser provider for download and installation instructions.
December 14, 2021
Nippon Telegraph and Telephone Corporation
Detection of graphene's divergent orbital diamagnetism at the Dirac point
-Paving the way to reveal novel properties and functionalities in graphene-
[Overview]
Nippon Telegraph and Telephone Corporation (NTT), University Paris-Saclay, CEA-Saclay, Néel Institute and National Institute for Materials Science (NIMS) have collaboratively succeeded in detecting divergent orbital diamagnetism in monolayer graphene at the charge-neutral (Dirac) point. It corroborates an important role of the topological phase*1 (Berry phase) in condensed matter physics.
Diamagnetism is a phenomenon where a magnetization emerges in a material opposite to the externally applied magnetic field. Graphene is a one-atom-thick limit of graphite, and it has a unique relation between the energy and momentum of an electron, forming a cone-like shape between them (Fig. 1). Especially, there is a point called "Dirac point", where the two cones touch with each other. The Dirac point behaves as a topologically anomalous point and has been predicted theoretically to be essential to generate divergent diamagnetism.
In this study, extremely clean graphene encapsulated by hexagonal boron-nitride (hBN) and highly sensitive magnetic sensors employing the giant-magnetoresistance (GMR) effect*2 have enabled to detect a large diamagnetic signal at the Dirac point. Since the divergent diamagnetism arises from the topological phase at the Dirac point, this experimental observation demonstrates a crucial role of the topological phase in graphene. Furthermore, our experimental techniques are applicable to diverse materials other than graphene, therefore expected to contribute to explore novel phenomena driven by a nontrivial topological phase in topological materials*3.
1. Background
Diamagnetism in graphene has been intensively studied for more than 60 years. Theoretically, it is predicted that the diamagnetic response becomes infinite at the Dirac point in ideal graphene with no disorder and at the zero temperature. On the contrary, because of a finite level of disorder and finite temperature, experimental demonstration of the divergent diamagnetism in graphene remained difficult. Recent theoretical studies revealed that the topological phase, which originates from the unique band structure*4 of a material, is essential to determine its electrical and optical properties. Because divergent diamagnetism in graphene is one of the representative examples to show the role of the topological phase in a realistic material, its detection has long been expected.
2. Results
The joint research group successfully fabricated extremely clean graphene by encapsulating it with two atomically flat hBN. We mounted this graphene heterostructure on the top of GMR-based magnetic sensors and attempted to measure a diamagnetic signal (Schematic illustration of the study). When a diamagnetic response emerges, a loop of an electron orbit in graphene generates a magnetic field. The in-plane component of this magnetic field affects the direction of the magnetization in a ferromagnetic layer in the GMR device. Due to the variation of the resistance depending on the relative direction of the magnetization between the two ferromagnetic layers of the GMR device, it is possible to detect the diamagnetic response electrically (Fig. 2). In the actual experiments, an external magnetic field was applied normal to graphene and by detecting the change of the resistance of the GMR devices, we measured a magnetic field generated by a diamagnetic response. From the obtained electrical signals, we succeeded in showing that a large diamagnetic response emerges at the Dirac point (Fig. 3). These experimental results are in good agreement with the theoretical calculations accounting for our device geometries.
3. Technical points
Our successful experimental observation became possible using ultraclean graphene encapsulated by atomically flat hBN (Fig. 4). In addition, the elaborate detection setup is a key: Since a magnetic field generated by a diamagnetic response is normal to the graphene plane, it seems appropriate to attempt to detect the normal component of the generated magnetic field. However, because a large perpendicular external magnetic field is necessary to obtain a diamagnetic response itself, the normal component of a small diamagnetic field is overwhelmed by the large external field and difficult to detect. In this study, we focused not on the normal but on the in-plane component of the diamagnetic field and detected it by the GMR devices, which enabled the detection of the diamagnetic response in graphene.
4. Future developments
Our experimental observation of divergent diamagnetism in graphene unequivocally shows the importance of the topological phase in condensed matter physics. Application of this experimental technique to other novel materials accelerates to reveal unique properties in topologically nontrivial materials.
5. Publication Details
| Journal: | Science |
| Title: | "Detection of graphene's divergent orbital diamagnetism at the Dirac point" |
| Authors: | J. Vallejo, N.J. Wu, C. Fermon, M. Pannetier-Lecoeur, T. Wakamura, K. Watanabe, T. Taniguchi, T. Pellegrin, A. Bernard, S. Daddinounou, V. Bouchiat, S. Guéron, 1 M. Ferrier, G. Montambaux, H. Bouchiat |
6.Glossary of terms
1.Topological phase
It is also called "Berry phase". Electrons have both a particle-like and wave-like nature, and the wave function of electrons has the phase component. Suppose the state of an electron is adiabatically transformed from the initial state A into the same state (let us define it as A') by changing a parameter on which the wave function of the electron depends. In this case, while the electron finally returned to the same state, its wave function acquires an additional phase which depends on the trajectory between A and A' in the parameter space. In our experimental situation, the transformation from A to A' corresponds to the closed orbit of the electron's wave function due to the cyclotron rotational motion driven by the external magnetic field. In graphene, an electron acquires pi phase when it circulates once around the Dirac point.
2.Giant-magnetoresistance effect
It is the effect where the perpendicular resistance of ferromagnet/paramagnet/ferromanget trilayer structures changes depending on the relative direction of the magnetization in the two ferromagnetic layers. Usually the magnetization of the one of the ferromagnets is pinned and the other is left free to change.
3.Topological materials
Materials groups with topologically nontrivial band structures (see 4). Their topological nature is categorized by the topological number. Topological insulators epitomize topological materials, which have insulating bulk and conductive surfaces or edges.
4.Band structure
It represents the relation between the energy and momentum of electrons, and determines electrical properties of materials. Since materials consist of a periodic array of atoms, the periodic potential induced by these atoms provide the band structure of each material.
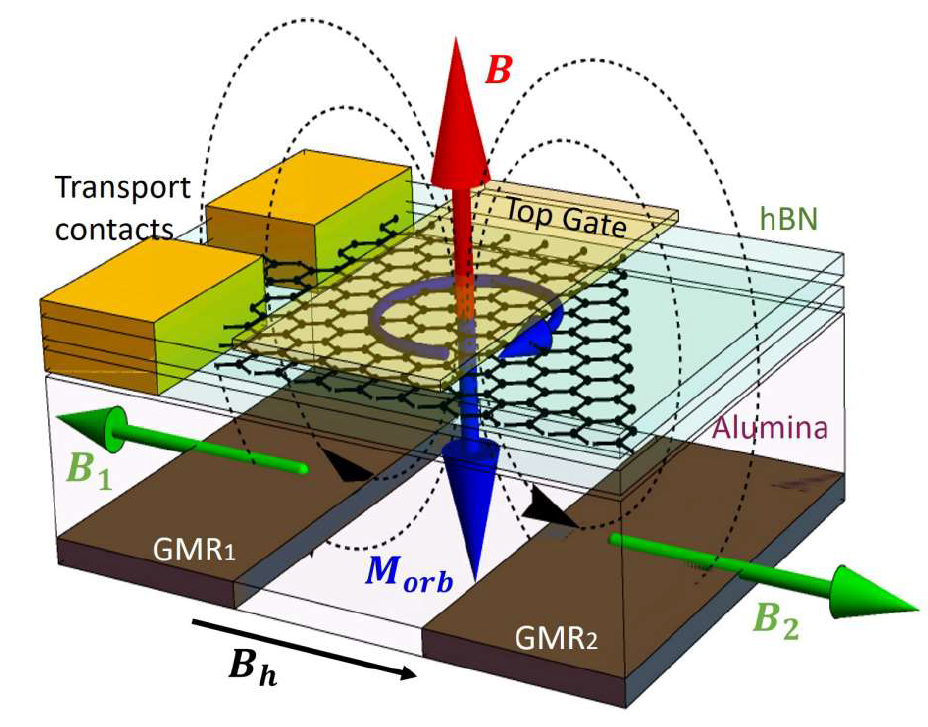 Schematic illustration of the study: Detection of divergent orbital diamagnetism in monolayer graphene by the GMR-based magnetic sensors.
Schematic illustration of the study: Detection of divergent orbital diamagnetism in monolayer graphene by the GMR-based magnetic sensors.
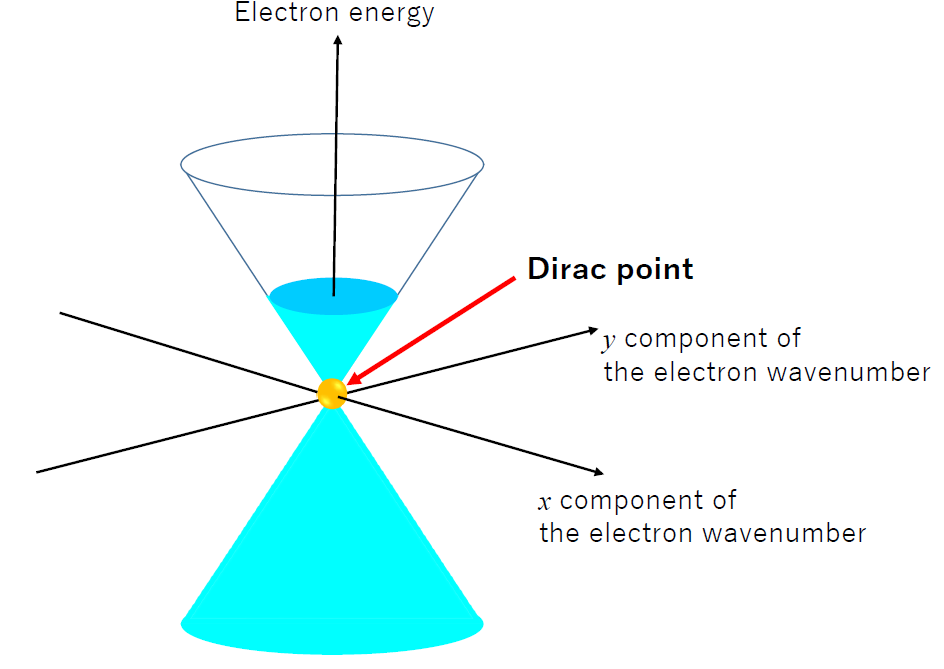 Fig. 1: Dispersion relation between the electron energy and momentum (wavenumber) in graphene. Electron density and charge polarization (electron or hole) can be modulated by the gate voltage. The Dirac point is located in the middle of electron- and hole-doped region.
Fig. 1: Dispersion relation between the electron energy and momentum (wavenumber) in graphene. Electron density and charge polarization (electron or hole) can be modulated by the gate voltage. The Dirac point is located in the middle of electron- and hole-doped region.
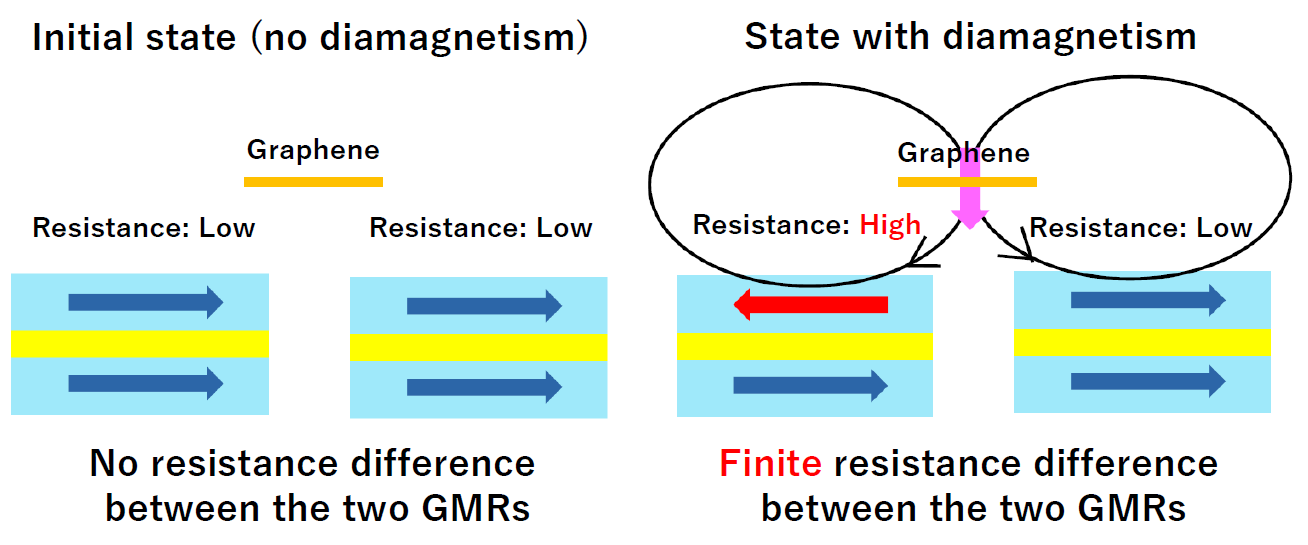 Fig. 2: Sketch of the electrical detection of diamagnetism using the GMR-based magnetic sensors.
Fig. 2: Sketch of the electrical detection of diamagnetism using the GMR-based magnetic sensors.
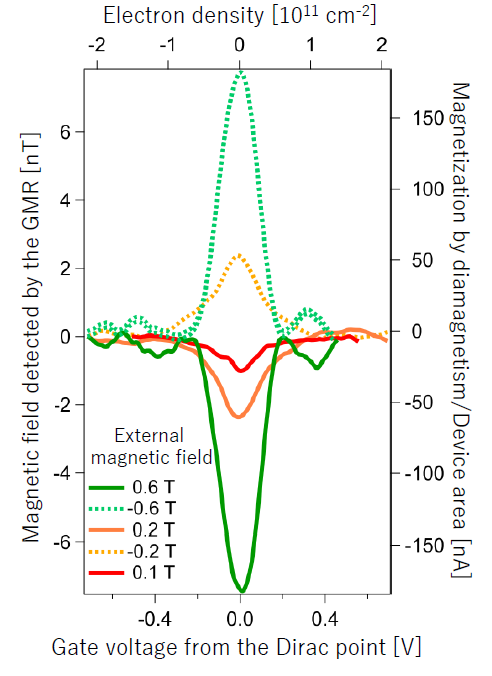 Fig. 3: Magnetic field due to the diamagnetic response detected by the GMR device and the magnetization converted from the magnetic field.
Fig. 3: Magnetic field due to the diamagnetic response detected by the GMR device and the magnetization converted from the magnetic field.
 Fig. 4: Optical microscope image of the device. Graphene is encapsulated by hBN and deposited on the top of the GMR-based magnetic sensors.
Fig. 4: Optical microscope image of the device. Graphene is encapsulated by hBN and deposited on the top of the GMR-based magnetic sensors.
For media inquiries regarding this matter, please contact
Public Relations Office
NTT Science and Core Technology Laboratory Group
science_coretech-pr-ml@hco.ntt.co.jp
Tel.: 046-240-5157
Information is current as of the date of issue of the individual press release.
Please be advised that information may be outdated after that point.
NTT STORY
WEB media that thinks about the future with NTT









