Technology to Dramatically Reduce the Scale of Practical Fault-Tolerant Quantum Computers
~The first hybrid quantum error correction/suppression scheme in the world~

Researchers at Nippon Telegraph and Telephone Corporation (NTT; head office: Chiyoda-ku, Tokyo; president: Jun Sawada; hereinafter "NTT"), in collaboration with the Center for Quantum Information and Quantum Biology, Osaka University (QIQB), have proposed a hybrid quantum error reduction technique, consisting of quantum error correction and quantum error mitigation. This novel method allows for the reduction of the size of quantum computers required for practical applications by up to 80%.

1. Introduction

Quantum computing is a new paradigm that performs computation by exploiting "qubits", which have unique properties of quantum mechanics such as superposition and quantum entanglement. Because quantum computing may solve prime number factorization and simulate chemical materials much more efficiently than classical computers, it has been extensively studied over the globe. Since superposition states are quite fragile against environmental noise, the biggest challenge towards the realization of quantum computers is the suppression of noise and the improvement of computation accuracy.

There are two distinct types of error suppression technologies: quantum error correction (QEC) and quantum error mitigation (QEM). QEC can correct computation errors by detecting errors and adaptively correcting them, by representing logical qubits with redundant physical qubits. Although QEC can suppress computation errors to an arbitrary level by using a large code size, it is evaluated that as many as 10 millions of physical qubits are required for practical applications - this seems decades away. The alternative method for error suppression is QEM, which relies on statistical methods to estimate the correct outcomes from the noise-free quantum computers; accordingly, it does not require encoding of qubits, implying hardware overhead is low. Therefore, QEM is a suitable error reduction technology for small-size current quantum computers. However, the statistical uncertainty of the estimated outcomes becomes prohibitively large when the number of errors during quantum computation increases. For this reason, QEM has been considered unavailable for medium or large-size quantum computers.

Because QEC is only useful for large-size quantum computers while applicable scales of quantum computers for QEM is restricted, efficient error reduction technique for medium-scale quantum computers has been missing; therefore, it has been believed that the realization of practical quantum computing is beyond reach.

2. Outline of our method

A research team in NTT has successfully integrated QEM and QEC, which have been independently investigated from distinct scenarios, and proposed a hybrid quantum error reduction method for dramatically improving computation accuracy in medium-scale quantum computing. In this research, the reduction of necessary physical qubits up to 80 percent is also reported. This method is expected to hasten the arrival of practical quantum computing, as well as unravel the new direction of research for fault-tolerant quantum computing, where the hybridization of error reduction techniques plays the crucial role.

3. Features of the technology

The key of this research is the dual error reduction structure, where easy-to-implement QEC first suppresses the error---subsequently, QEM removes the remaining errors (Fig. 1). While QEM usually requires additional operations on quantum computers, implementable operations on an encoded space when using QEC are quite restricted. Thus, it was highly non-trivial whether we can achieve a good balance between QEC and QEM. In this research, we employed probabilistic error cancellation method as a QEM method, which allows for efficient reduction of noise only by slightly changing the information processing of classical computers for QEC. Since the modifications of the information processing of classical computers are much easier than that on quantum computers, the dual error reduction method can be implemented with low overheads. By adopting this method, because the remaining errors which cannot be eliminated by QEC can be compensated by QEM, we can reduce the redundancy of physical qubits required for QEC, leading to the significant reduction of required computing resources.

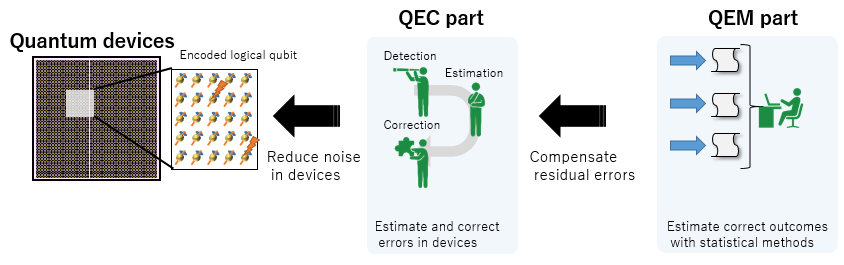Fig. 1. A schematic diagram of the porposed methods.

4. Future perspectives

The accomplishments of this research have shed new light on the field of error reduction of quantum computers and may completely change conventional ideas that QEM should be performed on small-scale quantum processors with QEC being applied to large-scale quantum computers. Since this method can be implemented to fault-tolerant quantum computers almost without inducing additional computation burdens, a broad range of conventionally assumed hardware requirements towards the realization of quantum computers can be dramatically reduced. Furthermore, other QEM methods rather than probabilistic error cancellation can be considered, which may further enhance the efficacy of the computation. QEM on the top of QEC can be used not only to reduce computation errors, but also to lighten the load of some operations in quantum computation and to reduce the communication load in distributed quantum computers, and thus has wide applications in compiler optimization for quantum computers. Thus, the guidelines provided by this research will play an important role towards the early realization of practical quantum computers.

5. Funding

This research has been made possible thanks to the support of the following funding: PRESTO, JST, Grants No. JPMJPR1916 and No. JPMJPR2114; ERATO, JST, Grant No. JPMJER1601; CREST, JST, Grant No. JPMJCR1771; MEXT Q-LEAP Grants No. JPMXS0120319794 and JPMXS0118068682; Moonshot R&D, JST, Grant No. JPMJMS2061.

Moonshot R&D Project Koashi PM commented:

It has been widely believed that the small-scale quantum computers that are being realized today and the large-scale quantum computers in the future completely differ and require distinct technological approaches, but this discovery has changed that conventional view. This finding shows that the technology developed for small-scale quantum computers can be useful even for developing a large-scale quantum computer. This paves the way for accelerating the progress toward the realization of an error-resistant general-purpose quantum computer, which is the goal of the Moonshot project.