Suppressing Hardware and Algorithm Errors in Quantum Computers
〜A general framework for increasing the precision of quantum operations〜

1. Key points

2. Overview

Research Associate Nobuyuki Yoshioka of Graduate School of Engineering at the University of Tokyo, Distinguished Researcher Yuuki Tokunaga, Researcher Yasunari Suzuki, and Researcher Suguru Endo of NTT Computer & Data Science Laboratories, Senior Researcher Yuichiro Matsuzaki of the National Institute of Advanced Industrial Science and Technology, and Specially Appointed Assistant Professor Hideaki Hakoshima of the Center for Quantum Information and Quantum Biology at Osaka University (full-time) have developed an efficient method to eliminate errors from unknown noise sources when performing quantum many-body computation algorithms with quantum computers.

Quantum computer is a general term for devices that perform calculations by exploiting superposition of quantum states and their interference (Note 4). To precisely perform calculations using a quantum computer, a number of technical obstacles must be overcome. The most important one is the suppression of errors caused by interactions with the external environment and imperfections in the hardware. Therefore, developing efficient computational methods that are effective even in resource-limited devices, in which, for example, the number of qubits (Note 5) is restricted, is quite urgent. However, from a practical standpoint, these methods are still in the early stages of development.

The research group has discovered that if multiple quantum states affected by unknown noise sources are prepared in parallel and then interfered with each other, both the effects of noise in the hardware and the errors inherent in the algorithm itself can be suppressed. The new framework minimizes the burden on hardware and suppresses computational errors. This method is expected to be very powerful for quantum computers that are equipped with many qubits with relatively low computation accuracy. This research has published in the online edition of the American scientific journal Physical Review Letters on July 6, 2022 (EDT).

3. Contents:

Background

Natural phenomena on the microscopic scale involving electrons and atoms are governed by quantum mechanics. As a familiar example, a quantum mechanical description is essential to understanding the principles of operation of components and materials such as transistors and semiconductors. In other words, quantum mechanics lurks everywhere in electronic devices such as personal computers and smartphones, which form the basis of modern information technology.

If the range of control by quantum mechanics is not limited to individual components of the device but extended to the operating principle of the entire device, it would be possible to dramatically improve computing performance. Such a seemingly far-fetched idea was proposed by American physicist Richard P. Feynman (Note 6) in 1982. The quantum computer is a generic name for a device that performs calculations by using the superposition of quantum states and their interference. It has been theoretically proven that if it becomes possible to completely control the inputs and operations of a quantum computer, it will be possible to accelerate the algorithms required for machine learning and material search. Although the idea was a pipe dream when it was first proposed, it has attracted significant attention because recent developments in quantum technology have gradually made it more and more feasible.

The most significant barrier to the precise execution of operations is the suppression of error caused by interactions with the external environment and hardware imperfections. Under the condition of the limited number of quantum gates and qubits (Note 5), the methods to efficiently increase precision have been sought for. In particular, how to eliminate the effects of noise when no information about the noise is available at all is a challenge in utilizing intermediate-scale quantum (NISQ) computers which suffer from noise.

Our research:

The joint research team found that even noise from unknown origin can be canceled by preparing multiple noisy quantum states in parallel and allowing them to interfere with each other. In particular, errors in the simulation of energy eigenstates of quantum many-body systems (Note 2) can be efficiently suppressed (Figure 1).

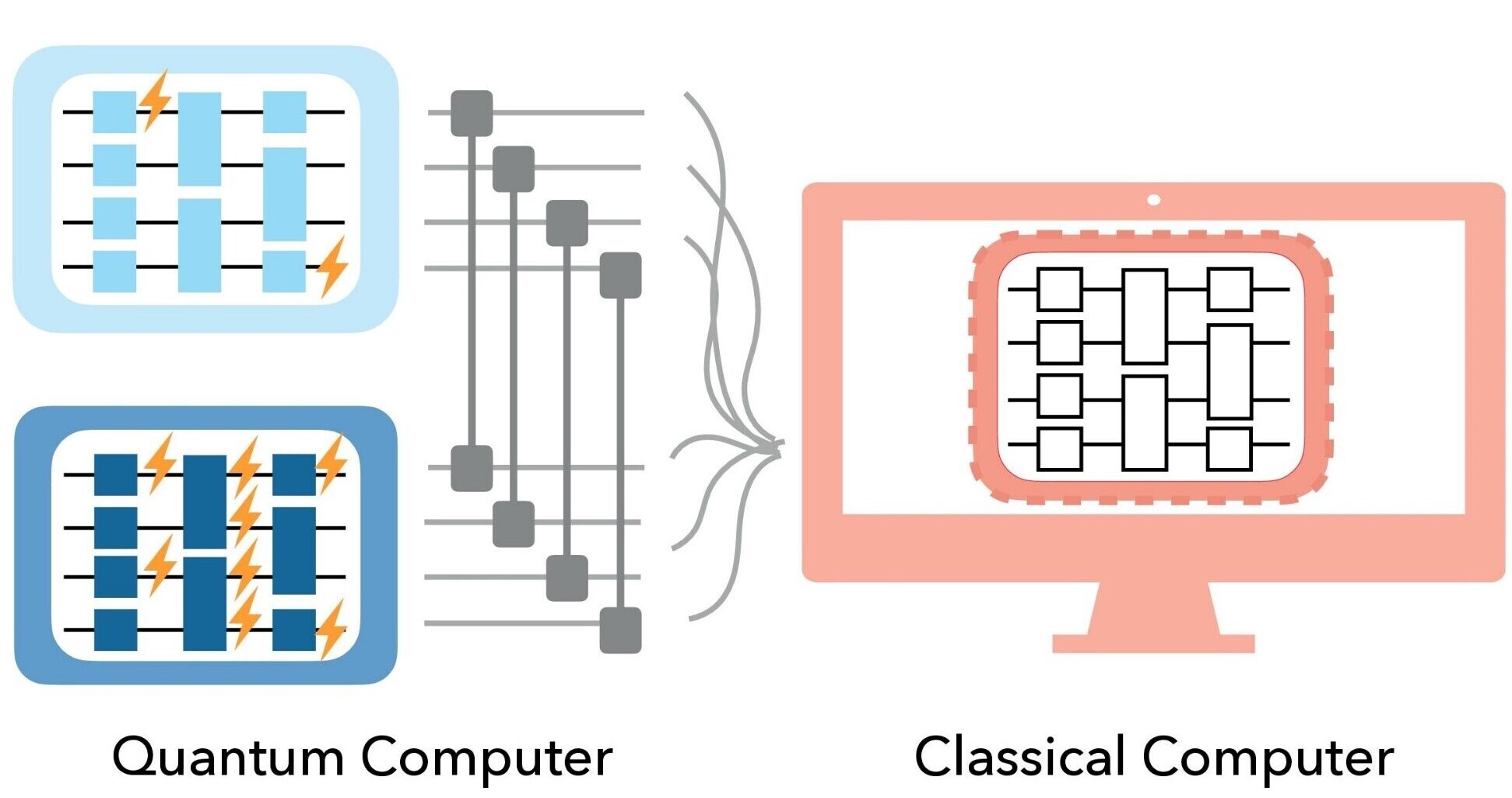Figure 1

Energy eigenstates are states that do not evolve in time under the Schrödinger equation, the fundamental equation of quantum mechanics. Calculation of energy eigenstates is essential for understanding quantum many-body phenomena, including condensed matter physics, quantum chemistry, and particle physics. For this reason, it is one of the most important topics among the applications of quantum computing.

In variational quantum algorithms (Note 7) for calculating energy eigenstates, such as variational quantum eigenvalue solvers (VQE), the wavefunction (Note 8) to be computed was mainly embedded directly into the quantum computer. In other words, the objective was to reproduce the quantum state to be computed inside the quantum computer. On the other hand, what is ultimately important in investigating quantum many-body systems is to extract the properties of the quantum state, not to directly realize the state. In fact, a series of methods called quantum error mitigation, which have been proposed to suppress computational errors while minimizing the load on the quantum hardware, are based on the idea of extracting high-precision results by combining low-precision calculation results.

The problem lies in the fact that depending on how the low-precision computation results are combined, a completely meaningless answer may be obtained. The focus is on how to efficiently eliminate errors while selecting mathematically valid combinations. The research team has now proposed the "generalized quantum subspace expansion method," which integrates multiple quantum error mitigation methods proposed so far in the most general form by extending the framework called the "quantum subspace expansion method" (Note 9).

One situation in which the effect is most pronounced is when multiple noisy quantum states are prepared. For example, different types of noisy quantum states are interfered with each other just before reading out the result. Combining the results of calculations obtained in such a situation simultaneously suppresses both hardware- and algorithm-derived noise, and enables more precise calculations than conventional methods such as quantum subspace expansion and virtual distillation (Note 10) (Figure 2). The results showed that when the VQE is performed, the calculations are much more precise than with conventional methods (Figure 3).

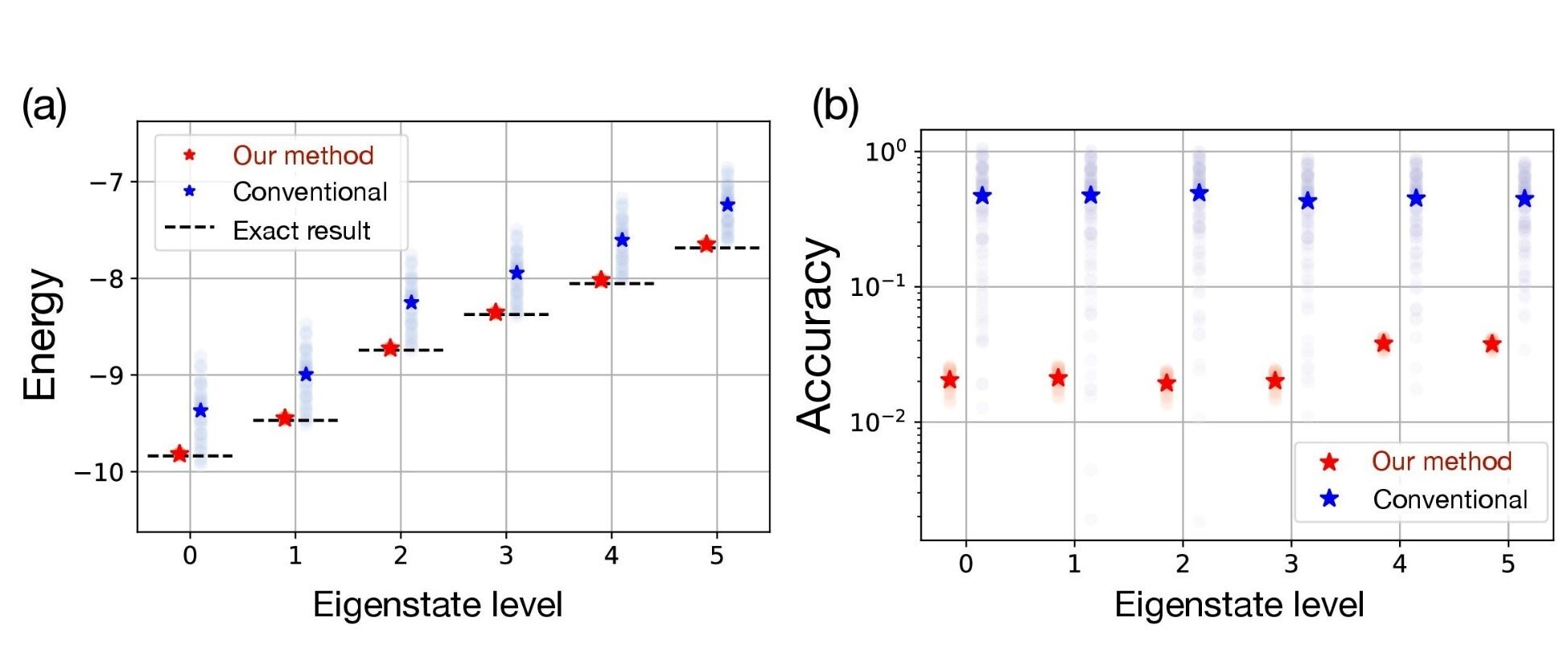Figure 2

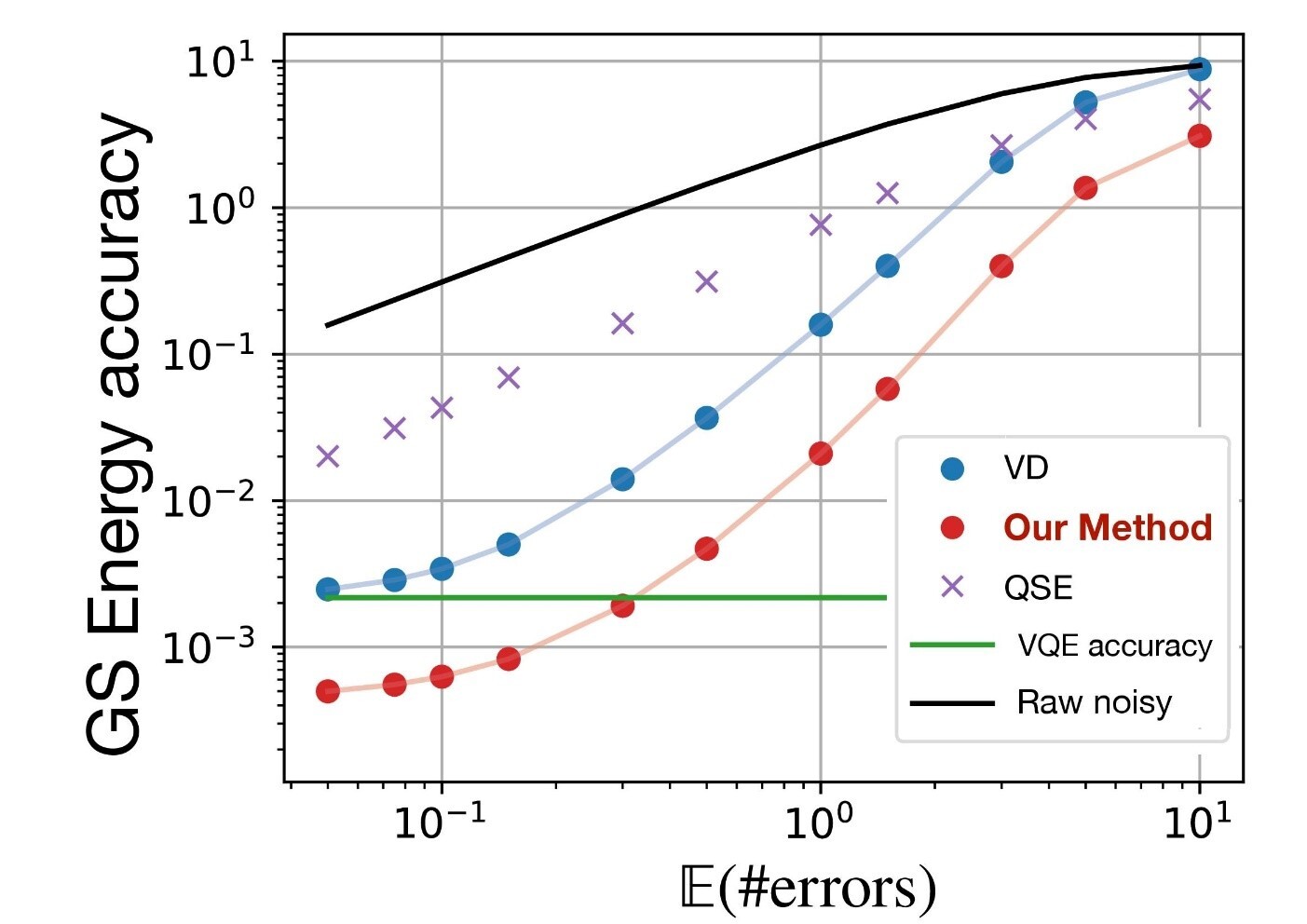Figure 3

Impact on society and future plans:

This research is an important step toward more robust use of quantum computers with limited resources such as the number of operations. Future directions include the extension to quantum many-body calculations other than energy eigenstates such as real-time evolution, the development of implementation methods for calculations based on quantum error correction (Note 11), and the development of methods to investigate the nature of noise itself using this method.
　If the development of these methods can provide a computational advantage using quantum algorithms, they are expected to contribute to improving the efficiency of computation in a wide range of fields, including basic science, machine learning, and materials science.

Funding:

This work was supported by the Leading Initiative for Excellent Young Researchers MEXT Japan and JST presto (Grant No. JPMJPR1919) Japan. This work was partly based on results obtained from a project, JPNP16007, commissioned by the New Energy and Industrial Technology Development Organization (NEDO), Japan. This work is supported by PRESTO, JST, Grants No. JPMJPR1916, No. JPMJPR2114, No. JPMJPR2119; ERATO, JST, Grant No. JPMJER1601; MEXT Q-LEAP Grants No. JPMXS0120319794 and No. JPMXS0118068682. This work also was supported by JST [Moonshot R&D] [Grant No. JPMJMS2061]. This work was supported by JST COI-NEXT program (JPMJPF2014).

Published journal:

Journal's name: Physical Review Letters
Title: Generalized Quantum Subspace Expansion
Authors: Nobuyuki Yoshioka, Hideaki Hakoshima, Yuichiro Matsuzaki, Yuuki Tokunaga, Yasunari Suzuki, Suguru Endo
DOI: 10.1103/PhysRevLett.129.020502
URL: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.020502

Authors: Nobuyuki Yoshioka, Research Associate , Graduate School of Engineering, the University of Tokyo
Hideaki Hakoshima , Specially Appointed Assistant Professor, Center for Quantum Information and Quantum Biology, Osaka University
Yuichiro Matsuzaki , Senior Researcher, National Institute of Advanced Industrial Science and Technology
Yuuki Tokunaga, Distinguished Researcher, NTT Computer & Data Science Laboratories
Yasunari Suzuki , Researcher, NTT Computer & Data Science Laboratories
Suguru Endo, Researcher, NTT Computer & Data Science Laboratories

8. Terminology

^{(Note 1)}Quantum computer: A computer in which the control of operations is based on quantum mechanical principles. Conventional computers are distinguished as "classical computers" because they are based on classical mechanical principles.

^{(Note 2)}Quantum many-body system, quantum many-body computation: A quantum many-body system is a system in which a large number of particles interact with each other according to quantum mechanics, or a system that models the nature of such interaction. Quantum many-body computation refers to the simulation of quantum many-body systems.

^{(Note 3)}Quantum entanglement: A correlation that cannot be explained only by classical mechanics. It is also called entanglement.

^{(Note 4)}Interference: A change of quantum states obeying quantum mechanics through the interaction between systems.

^{(Note 5)}Quantum bit, quantum gate: The smallest unit of information that constitutes a quantum computer is called a qubit, and the operation that acts on a qubit is called a quantum gate.

^{(Note 6)}Richard P. Feynman (1918 - 1988): American theoretical physicist. He invented the Feynman diagram, which calculates the reaction processes of elementary particles. He was awarded the Nobel Prize in Physics in 1965 for his significant contributions to the development of quantum electrodynamics.

^{(Note 7)}Variational quantum algorithm: An algorithm that approximates a desired operation by sequentially updating the type of quantum gate based on the measurement results of a quantum computer. It is counted as one of the quantum-classical hybrid algorithms, since it involves the cooperation of a quantum computer and a classical computer. Variational Quantum Eigensolver (VQE) is a typical example.

^{(Note 8)}Wave function: A mathematical expression of a quantum state using complex amplitudes.

^{(Note 9)}Quantum subspace expansion method: One of the quantum many-body calculation methods using quantum computers. Instead of directly realizing the desired quantum state on a quantum computer, a part of the superposition (subspace expansion) is expressed by utilizing a classical computer.

^{(Note 10)}Virtual distillation method: One of the error mitigation methods in quantum computers. It refers to an operation in which copies of quantum states that have been "mixed" due to noise are distilled into "pure" quantum states by interfering with each other.

^{(Note 11)}Quantum error correction: A method of controlling errors in quantum computers. By combining multiple qubits, error-tolerant qubits are configured due to redundancy.

^{Figure 1:}Conceptual diagram of a quantum many-body calculation using multiple quantum states with different noise intensities. In the method proposed in this study, the appropriate method of combining the results of interfering multiple states is computed on a classical computer in an auxiliary manner before outputting the final calculation results.

^{Figure 2:}(a) calculated eigenenergies and (b) their accuracy under imperfect noise intensity control. While the accuracy of the calculation deteriorates as the conventional method reflects fluctuations in the control, the present method is almost unaffected, and is expected to perform robustly in actual experiments.

^{Figure 3:}Calculation accuracy of a variational quantum eigenvalue solver (VQE), a type of variational quantum algorithm, when the operation itself is incomplete and noise is generated on the quantum computer. When the number of generated errors is about 1 or less, the calculated energy accuracy differs significantly. In other words, it can be read that the performance difference by the error suppression method is remarkable. In particular, when this method is used, the calculation is more accurate than the calculation of the VQE itself. In other words, the errors inherent in VQE can also be suppressed. This is an area that cannot be achieved by conventional methods such as the virtual distillation method or the quantum subspace expansion method.