Physical Deep Learning by Novel Brain-Inspired Training Algorithm
～Proposed Algorithm Enables Accelerated Photonic Deep Learning～

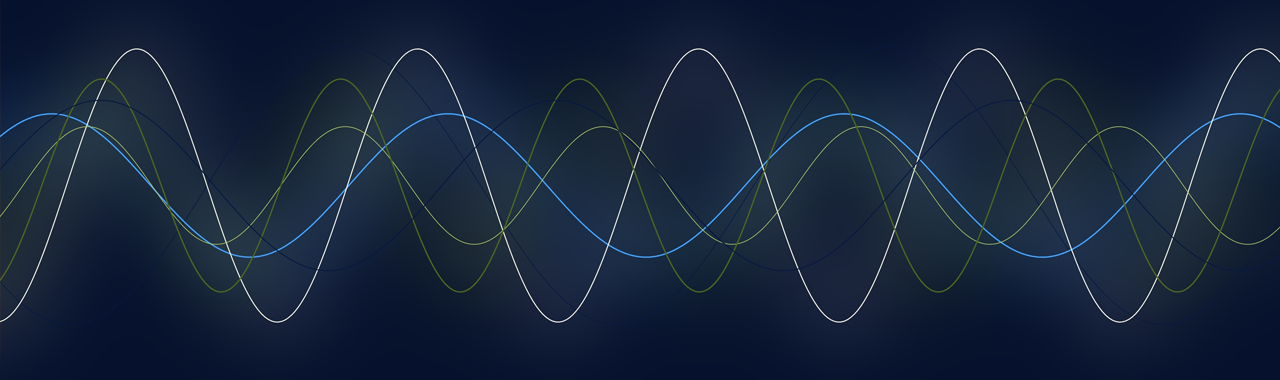
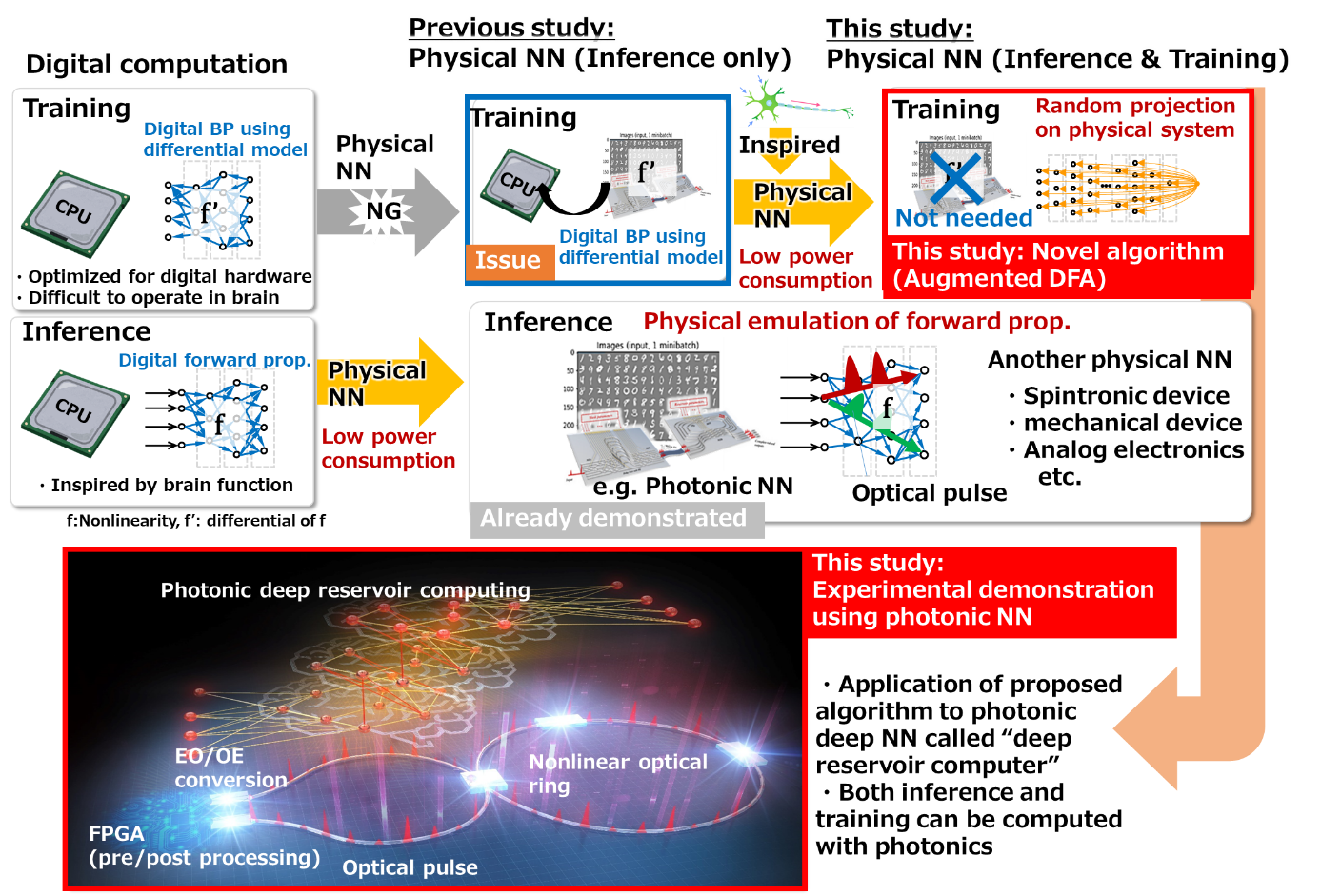Figure 1: (Top) Explanation of our achievement. Conventionally, computation for NN training is performed on standard digital computers even in the case of physical NNs. Here, we propose a novel training algorithm which can be efficiently executed on physical hardware. (Bottom) Overview of our constructed photonic NN system for demonstration. A special type of deep recurrent neural network (*4), called deep reservoir computing (*3), was implemented on this system. In this system, optical pulses in nonlinear optical rings are considered as neurons of the reservoir computer. The output signal from the optical ring is re-input to the same optical system, which emulates the "deep" connection of the network. Computations for inference and for training are performed on the same system, which is assisted by photonic computations on the nonlinear rings.

1. Introduction

Recent advances in artificial intelligence (AI) technologies have enabled outstanding information processing, such as for machine translation, automated driving, and robot control, but at the same time, the power consumption and computational time for executing huge-scale deep NN models have increased drastically. As these increments will be beyond the capacity of conventional computing hardware, drastic improvement of computational hardware efficiency is highly required.
　Physical NNs, which are classified as neuromorphic devices (*6), are gathering attention as alternative hardware for future computational engines for AI processing. In this framework, we consider a physical system as a physically constructed NN; i.e., physical nonlinearity corresponds to activation of neurons, and the response of the physical system corresponds to the computational result of a specific NN. In particular, physical NNs using an optical system, called photonic NNs, are attracting much attention due to their potential for low latency and low power consumption. The training (*7) of deep NNs has basically relied on a method called backpropagation (BP, *8), which has seen great success in standard (not physical) NNs. This approach requires accurate knowledge about the deep NN of interest, such as the learning parameters (*9) and nonlinearities, and their derivative values. Such information can be easily accessed with a standard computer. However, when we use BP to train a physical NN, we need to accurately measure or simulate the physical system and its derivatives in order to obtain all the information on it. This complexity results in a loss of any advantage in speed or energy associated with using the physical NN in the training process. Thus, it greatly limits the scalability and effectiveness of physical NNs.
　Like BP in physical NNs, the operational difficulty of BP in biological neurons has also been pointed out in the brain science field; the plausibility of BP in the brain — the most successful physical NN — has been doubted. This has motivated the development of alternative training algorithms that can be implemented on biological neurons.

2. Overview of achievement

In this study, inspired by such biologically motivated training algorithms, we developed a novel algorithm called "augmented direct feedback alignment (DFA)". The algorithm is highly suitable for physical NNs, including photonic ones, because it does not require an accurate understanding of the information in the physical system and its computation can be emulated on physical hardware.
　Figure 1 (top) shows an overview of the proposed method. Among the biologically motivated training algorithms, we focused DFA (*10), and extended it for implementation in physical NNs. The proposed method updates the training parameters based on a random projection of error signals (the difference between the output from NNs and the desired output). Unlike the BP method, these procedures do not require measurement or simulation of the physical system. In addition, the computation of augmented DFA can be executed on physical systems such as optical circuits, allowing efficient computation even in the training phase. The research also revealed that this new learning method is applicable to not only NN models oriented towards physical implementation, but also to various practical NN models. Furthermore, as a proof-of-concept demonstration, we constructed a photonic NN [Fig. 1 (bottom)] in which optical computation assists both inference and training computations. Using the constructed photonic system, we confirmed the potential of accelerated computation, including the training procedure, and achieved the highest performance in the physical NN field. Our results will contribute to the realization of photonic AI computation systems, which will drastically reduce the power consumption and computation time in future AI engines.

3. Technical points

(1) Physical NN oriented training algorithm: Augmented DFA

We focused on a biologically inspired training method called DFA, and augmented it for application to physical NNs. As shown in Figure 2(a), the conventional DFA method trains a deep NN by performing a random projection on the error signals, which simplifies the training procedure compared with BP. However, it still requires computation based on derivatives of nonlinearity in the physical NN. Here, we replaced it with an arbitrary nonlinear function. Owing to this augmentation, we no longer need to measure or simulate the physical system. In addition, we can execute this random nonlinear transformation procedure on a physical system, which enables the physical acceleration of both inference and training computations. We also found that the proposed augmented DFA is applicable to wide range of deep NN models, including recent practical NN models and NN models oriented for physical implementation [Figure 2(b)].

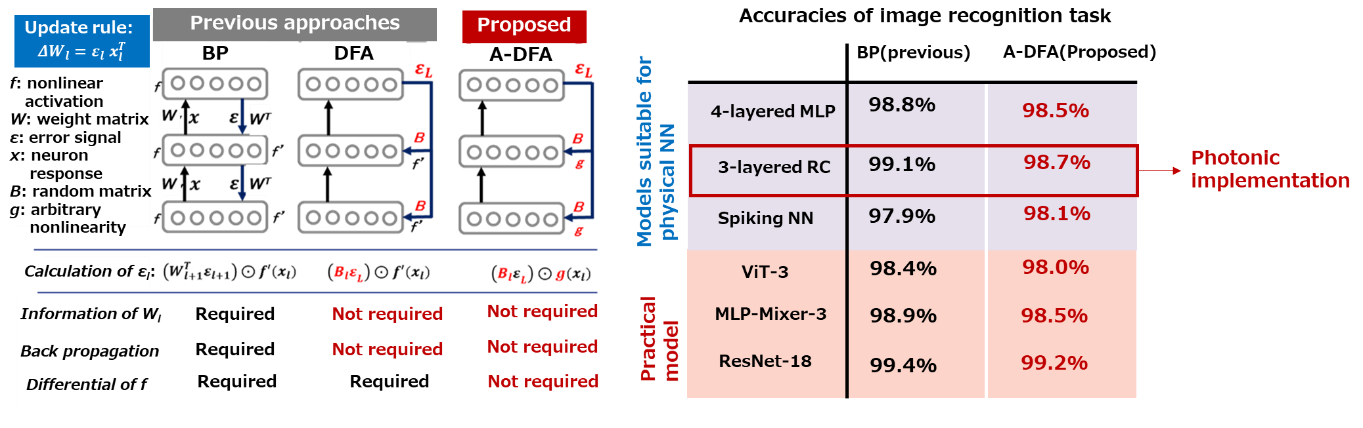Figure 2： (a) Overview of previous and proposed training methods; (b) benchmark results for various models. The task is image recognition of handwritten digits. To verify the applicability of the proposed method, we used a model that has been actively researched in physical implementation (blue hatch) and a model that is actually used in image recognition and other applications (red hatch). In both cases, the performance of the proposed method was equivalent to that of the BP method in this benchmark.

(2) Experimental demonstration using photonic NN

As a proof-of-concept demonstration with actual physical hardware, we constructed a photonic NN system emulating one type of deep NN model called a deep reservoir computer (*9). This was the world's first attempt to demonstrate accelerated computation using a photonic system, including all the processing for deep learning. In this circuit, the computation in the middle layer, called the reservoir layer, was performed in a nonlinear optical fiber loop with optical pulses used as the neurons in the NN model. The output signal was re-input to the same optical circuit to compute a deep NN model. While the input and output layer computations were performed on the electronic circuit [field-programmable gate array (FPGA)], the reservoir layer, which incurs heavy computational costs because it includes recurrent computation, was performed in the optical region. Besides the hardware, we also built a software stack to drive the above system, which enabled us to drive the photonic NN like a CPU, GPU, or other common computing devices. Thanks to this hardware/software implementation, we were able to compare the total computational speed of the photonic hardware with CPUs and GPUs.
　Figure 3(a) shows the results of comparing the performance of the constructed system on benchmark tasks of image processing. With the proposed algorithm, the constructed photonic NN achieved the best performance among other physical NNs. Figure 3(b) shows the measured training time per image for our constructed system as a function of the number of neurons. For comparison, we also show the results for augmented-DFA and BP training on a CPU and GPU. For small-scale network models, the computational speed of the constructed photonic hardware is limited by data transfer from the electronic to optical domain, which limits the advantage of optical computation. On the other hand, as the models become larger, a remarkable learning acceleration effect was observed with the use of optical NNs. This indicates that we can accelerate the computation of deep NNs using the photonic NN and proposed algorithm in the large-neuron-count region. As the power consumption of computation is determined by the product of efficiency and computation time, faster computation also contributes to lowering the power consumption of AI. This is the world's first demonstration of accelerated photonic deep learning that includes all the processing.

Figure 3: (a) Benchmark results from image recognition tasks (handwritten character recognition, clothes image recognition, and general image recognition) on the constructed optical NN. For reference, we show the results for optically implemented convolutional NN (CNN), multilayer perceptron (MLP), and reservoir computer (RC), as well as those of previous RC studies that used other physical systems. Traditionally, learning has been performed either by the BP method, which is very time-consuming for digital computation such as physical simulations, or by the least-squares method, which is not expected to provide sufficient recognition performance. The extended DFA method proposed in this study enables efficient and high-performance learning without information on the physical system. (b) Dependence of computation time per unit image on the number of neurons. In addition to the measured values for the optical NN (blue line), the learning time on a CPU (green and orange lines) and GPU (red line) are also shown for comparison. As the number of neurons increases, the learning acceleration effect of using optical NNs on conventional computers (CPU and GPU) is confirmed.

4．Outlook

We will continue to study the applicability of the methods proposed in this research to specific problems and investigate large-scale, compact integration of optical hardware. We aim to establish a high-speed, low-power optical computing infrastructure on optical networks that can fundamentally solve these problems, and apply it to solving various social issues for a safe, secure, and prosperous society.

Support for this research

Some of the results of this research were obtained with the support of Grants-in-Aid for Scientific Research (KAKENHI) (JP18H05472, JP20J12815, JP22K21295), the Japan Science and Technology Agency (JST) CREST (JPMJCR2014), and the New Energy and Industrial Technology Development Organization (NEDO) (JPNP16007).

Journal of Publication

Journal: Nature Communications (online edition, December 26)
Title: Physical Deep Learning with Biologically Inspired Training Method: Gradient-Free Approach for Physical Hardware
Authors: Mitsumasa Nakajima, Katsuma Inoue, Kenji Tanaka, Yasuo Kuniyoshi, Toshikazu Hashimoto, and Kohei Nakajima

Explanation of Terms

^*1.Deep neural network (deep NN)
A type of mathematical model inspired by information processing in the brain. It represents neural network-like connections of the brain with networked nodes and nonlinear transformations. A deep NN refers to a mathematical model consisting of multiple layers of NNs, and has the characteristic of being able to learn complex features through parameter optimization by learning.

^*2.Physical neural network (Physical NN)
A type of information processing framework that utilizes physical systems as NN computational elements. Information processing is performed by considering changes in various physical quantities that exist in nature, such as electric current, magnetic moment, structural displacement, and light intensity, within the physical system as the NN's computational process. Structural coupling within the physical system corresponds to interactions between neurons, and nonlinear responses correspond to nonlinearities of neurons.

^*3.Reservoir computing
A type of recurrent neural network (*4) with regression connections in the intermediate layer. It is characterized by randomly fixed connections in the intermediate layer, called the reservoir layer. In deep reservoir computing, the reservoir layer is connected in multiple layers to process information.

^*4.Recurrent neural networks
An NN with recurrent connections in the middle layer of the network, which excels in recognizing a series of data, such as time series data, because past information circulates inside the network. When processing image data, image pixels are arranged in chronological order for learning and inference.

^*5.Optical circuit
A circuit in which silicon or quartz optical waveguides are integrated on a silicon wafer using electronic circuit manufacturing technology. In telecommunications, optical communications paths are branched and merged by interference and wavelength-multiplexing of light. In optical computing, sum-of-products operations and other calculations are performed optically based on the same principle.

^*6.Neuromorphic device
A computational device that mimics the information processing of the brain. Originally, this term referred to devices that mimic the structure of the brain and the firing mechanisms of neurons with physical devices, but in recent years it has also included devices that efficiently compute deep NN calculations. In this paper, the term is used in the latter broad sense.

^*7. Training
Optimization is performed to obtain the correct output for an input based on a collection of data consisting of output pairs for known inputs for variables (learning parameters) included in a deep NN. This optimization process is called "learning", and the process of calculating the output from the given input data based on the optimized learning parameters is called "inference".

^*8.Back propagation (BP) method
The most commonly used learning algorithm in deep learning. While the error signal is propagated backward, the gradient of the weights (parameters) in the network is calculated, and the weights are updated so that the error becomes smaller. Since the back propagation process requires transposition operations of the weight matrix of the network model and differential operations for nonlinearity, it is generally difficult to execute on an analog computer.

^*9.Training parameters
Variables included in the deep NN that is the target of learning.

^*10.Direct feedback alignment (DFA) method
A method that calculates the error signals of each layer pseudoactively by performing a nonlinear random transformation of the error signal of the final layer. It does not require differential information of the network model, etc., and can be computed only by parallel random transformation, making it compatible with analog computation.