Timing attacks threaten cryptographic implementations, including Wi-Fi connection authentication. This highly efficient technique protects against them.
Developing a fast and secure algorithm for quadratic residuosity testing

Tokyo -November 27, 2023 - NTT Corporation (NTT), in collaboration with Aarhus University in Denmark, has developed a fast and versatile algorithm for quadratic residuosity testing^[1] in constant time, i.e., with execution time independent of the input. This technique thwarts so-called timing attacks, which use variation in computation time to steal secret information; as a result, it contributes to the fast and secure implementation of cryptographic functionalities such as distributed electronic signatures in blockchain, electronic passport authentication, and password-based key exchange in Wi-Fi routers. In particular, this result yields large speedups in the computation of hash functions to elliptic curves^[2], a widely-used cryptographic primitive, for which we obtain 2.5 to 3.5 times better performance than classical techniques (Figure 1) while ensuring a high level of implementation of security. We achieve even more dramatic speedups in settings that use larger parameters than conventional elliptic curve cryptography; this is for example the case for the post-quantum encryption scheme CTIDH^[3], in which the hash function to elliptic curves becomes up to 46 times faster.
　The paper^[4] will be presented at the ACM CCS 2023 conference held in Copenhagen, Denmark from November 26 to 30, 2023.

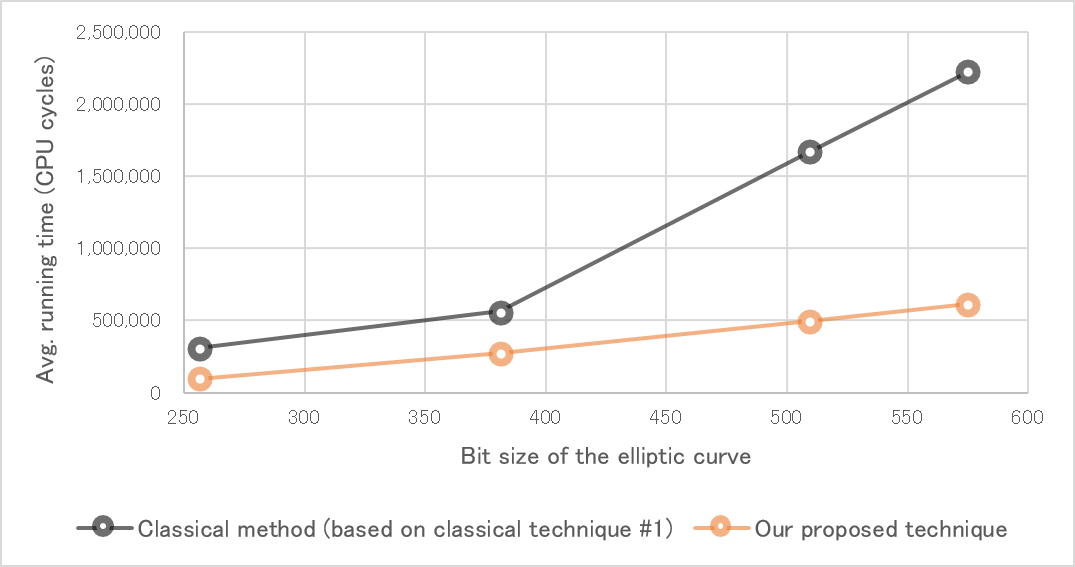Figure 1 Performance comparison of hashing to elliptic curves

1. Background

Elliptic curve cryptography, one of the most widely-deployed types of cryptography today, frequently relies on an operation that converts a secret value into a point on an elliptic curve (a so-called hash function to the elliptic curve). This is for example the case in the BLS digital signatures used in blockchain technology, in the password authenticated key exchange of electronic passports, and in the WPA3 standard that governs the most recent Wi-Fi routers. Hash functions to elliptic curves are also used beyond elliptic curve cryptography, e.g., in certain next-generation cryptographic schemes like the post-quantum encryption scheme CTIDH, which is based on elliptic curve isogenies, a new type of cryptographic assumption secure against quantum computers.
　In order to compute a hash function to an elliptic curve, one needs to test whether a certain integer value depending on the input of the hash is a quadratic residue with respect to a fixed prime number (one of the parameters of the elliptic curve): this amounts to checking whether one can find a multiple of the prime number which, when added to the integer, gives a perfect square. This is a fundamental problem in number theory than has been studied for over 200 years.
　Additionally, it is usually crucial that hash functions to elliptic curves are implemented in such a way that the execution time is constant, i.e., independent of the secret input value. Indeed, if the computation time varies depending on the input, the resulting scheme becomes vulnerable to "timing attacks", whereby an attacker measures the execution time and uses it to recover the secret input value. Such attacks have repeatedly proved devastating in practice, as evidenced by examples like Lucky Thirteen, a timing attack the TLS protocol (which protects the confidentiality of web traffic and most communications over the Internet) that fully decrypts communications in the presence of non-constant time key agreement, as well as a recent attack on the WPA3 standard of Wi-Fi routers^[5], which completely recovers Wi-Fi passwords due to non-constant time implementations of hashing to elliptic curves. It is therefore necessary to ensure that quadratic residuosity testing algorithm used inside the hash function to elliptic curves is also implemented in constant time.

2. Limitations of classical techniques

Traditionally, two main techniques have been used to test for quadratic residuosity. The first method is based on the law of quadratic reciprocity, which reduces the problem of testing whether a is a quadratic residue modulo p to quadratic residuosity testing modulo smaller primes (hereinafter, "classical technique #1"). This method is similar to the Euclidean algorithm for computing greatest common divisors and it is very fast; however, it is vulnerable to timing attacks because the number of execution steps (reductions to smaller primes), and hence the execution time, depends on the input a.
　On the other hand, another approach, based on Fermat's little theorem, reduces quadratic residue testing to the computation of an exponentiation modulo p (hereinafter, "classical techniques #2"). It is easy to implement the exponentiation algorithm in constant time independent of the input a, and hence ensure security against timing attacks, but this is a relatively heavy computation, resulting is dozens of times slower computation times for this techniques compared to classical technique #1.
　Thus, classical implementations of quadratic residuosity testing would typically need to choose between speed and security, not achieving both at the same time.

3. Points and Effects of the Technology

As mentioned above, existing techniques for quadratic residue determination can be roughly divided into algorithms based on classical technique #1, which is fast but vulnerable to timing attacks, and classical technique #2, which is safe to implement but slow. In contrast, our proposed technique provides a quadratic residuosity testing algorithm which is both safe and efficient (Figure 2).

As a result, we obtained essentially the same level of performance as the fast but vulnerable classical technique #1, while being as secure as the safe but slow classical technique #2 (Figure 2). In the computation of the hash function to elliptic curves used in BLS digital signatures, we observed a 2.5 to 3.5 times speedup over classical technique (Figure 1). The effect in the case of CTIDH, a post-quantum encryption scheme using elliptic curves with larger parameters, is even more impressive: the hash function to elliptic curves becomes up to 46 times faster.

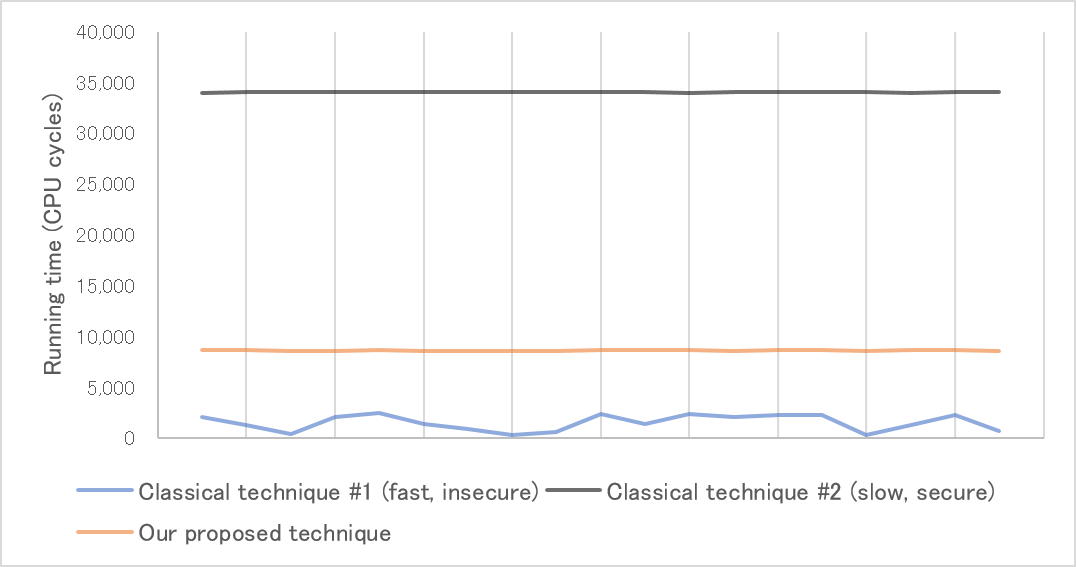Figure 2 Running time (y-axis) of the various quadratic residuosity testing algorithms modulo a 254-bit prime for random low-Hamming weight inputs (x-axis). Classical technique #1 is visibly not constant time (hence insecure), whereas classical technique #2 is secure but over three times slower than our proposed technique, also secure.

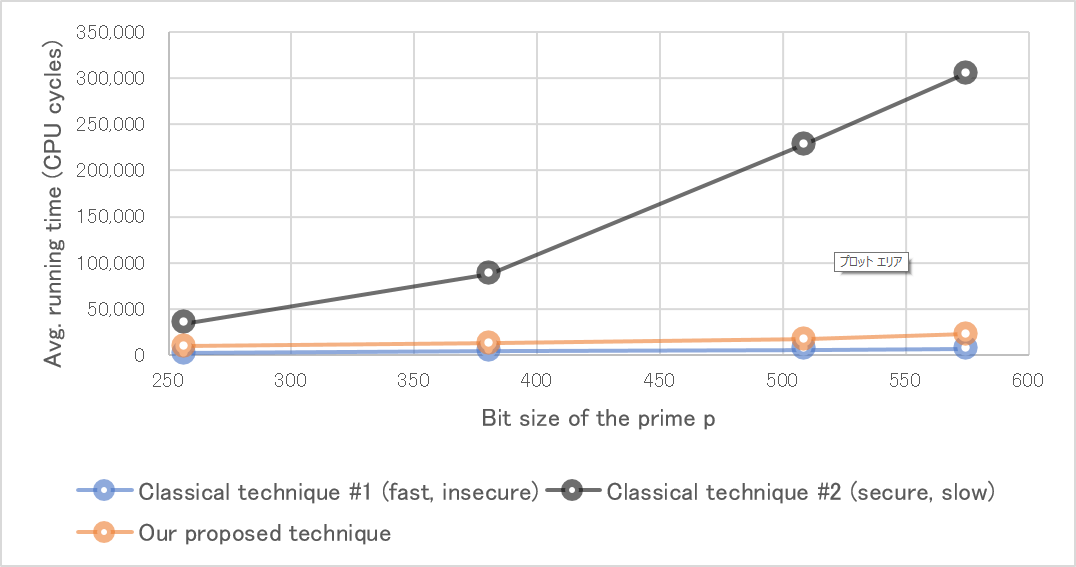Figure 3 Performance comparison of quadratic residuosity testing depending on parameter size

This novel algorithm for quadratic residuosity testing is compatible with, and can be used alongside, the significant improvement of hashing to elliptic curves presented by NTT (in collaboration with CINVESTAV and TII) at last year's ASIACRYPT 2022 international conference^[7], and which received the best paper award at that venue.

4. Outlook

This research result is a highly versatile technique that can be used in a plug-in fashion in all cryptographic implementations relying on quadratic residuosity testing, and particularly all implementations of hashing to elliptic curves regardless of the type and parameters of the curve. This achievement not only contributes to enhancing the performance and/or security against timing attacks of various cryptographic schemes in current use, but can also be expected to speed up and protect implementations of post-quantum cryptographic schemes to be deployed in the near future, and hence contribute to the necessary transition to these quantum-resistant technologies.
　NTT will continue to promote research and development in secure cryptographic implementations that achieve high levels of both safety and performance, and to foster foundational research with practical applicability.

^[1]The product of an integer with itself, such as 9=3×3 or 49=7×7, is called a perfect square. The remainder of a perfect square in the division by some prime number p is called a quadratic residue modulo p. For example, since the remainder of 9 in the division by 7 is 2, 2 is a quadratic residue modulo 7. On the other hand, one can prove that 3 is not a quadratic residue modulo 7. Determining whether a natural number a less than p is a quadratic residue modulo p is called quadratic residuosity testing. It is a basic mathematical operation needed in a wide range of cryptographic schemes, ranging from widely-used elliptic curve cryptography to some next-generation post-quantum schemes.

^[2]Elliptic curves are curves that form the "space of cryptographic computation" in most currently deployed cryptographic schemes. A hash function to an elliptic curve is a way to represent a message (such as a password or a key) as a point on an elliptic curve. It should satisfy various security properties, such as the fact that the point representing a message not seen before should look like a random point on the curve.

^[3]When large-scale quantum computers are built in the coming decades, practically all public-key cryptography technology in use today, including elliptic curve cryptography, will be effectively broken by a known quantum algorithm (Shor's algorithm). Therefore, the development and deployment of cryptographic scheme that are secure against quantum computers, known as "post-quantum cryptography", is a pressing issue in contemporary cryptography research. The CTIDH scheme, which is viewed as a strong candidate for post-quantum cryptography thanks to its very short key size and ciphertext size, also uses a hash function to elliptic curves, which can be dramatically accelerated by our proposed technique.

^[4]"Faster constant-time evaluation of the Kronecker symbol with application to elliptic curve hashing." Diego F. Aranha, Benjamin Salling Hvass, Bas Spitters, Mehdi Tibouchi. In ACM CCS 2023.

^[5]"Dragonblood: Analyzing the Dragonfly handshake of WPA3 and EAP-pwd." Mathy Vanhoef, Eyal Ronen. In IEEE Symposium on Security & Privacy 2020.

^[6]"Fast constant-time GCD computation and modular inversion." Daniel J. Bernstein, Bo-Yin Yang. IACR TCHES 2019(3):340-398, 2019.

^[7]"SwiftEC: Shallue-van de Woestijne indifferentiable function to elliptic curves." Jorge Chavez-Saab, Francisco Rodriguez-Henriquez, Mehdi Tibouchi. In ASIACRYPT 2022.

About NTT

NTT contributes to a sustainable society through the power of innovation. We are a leading global technology company providing services to consumers and business as a mobile operator, infrastructure, networks, applications, and consulting provider. Our offerings include digital business consulting, managed application services, workplace and cloud solutions, data center and edge computing, all supported by our deep global industry expertise. We are over $95B in revenue and 330,000 employees, with $3.6B in annual R&D investments. Our operations span across 80+ countries and regions, allowing us to serve clients in over 190 of them. We serve over 75% of Fortune Global 100 companies, thousands of other enterprise and government clients and millions of consumers.