Uncovering the Connection Between Independently Studied Models in Pure Mathematics and Quantum Optics

TOKYO - May 13, 2025 - NTT Corporation (Headquarters: Chiyoda, Tokyo; President and CEO: Akira Shimada; hereinafter "NTT") has uncovered a connection between models that have, until now, been studied independently in pure mathematics and in physics (quantum optics). In this study, we revealed a relationship between the non-commutative harmonic oscillator (NCHO)¹, a mathematical model developed from purely mathematical interest, and the quantum Rabi model (QRM)², a physical model that describes the interaction between light and matter. Until now, the NCHO and the quantum Rabi model have been explored independently in the fields of mathematics and physics, respectively. However, this research bridges these two domains by integrating insights from both, potentially advancing both areas of study.

This result was achieved by applying research originally conducted on pure mathematics at NTT Institute for Fundamental Mathematics. Meanwhile, the quantum Rabi model, which serves as a model for the basic building blocks of quantum computers using superconducting circuits, has been actively studied by NTT Basic Research Laboratories.
　Going forward, by combining theoretical and experimental efforts, we aim to realize new discoveries—such as implementing theoretically proposed computation methods on actual quantum devices.

This research will be showcased at the Open House 2025 of the NTT Communication Science Laboratories, held from May 20, 2025.

Background

The NTT Institute for Fundamental Mathematics (https://www.rd.ntt/e/ifm/), established in October 2021, is dedicated to developing foundational theories in modern mathematics, while also promoting research that provides fundamentally new perspectives for addressing the increasingly complex and diverse challenges facing society. As part of this mission, the center has advanced research on models describing light-matter interactions, particularly focusing on the quantum Rabi model (QRM) from the perspective of pure mathematics.

The QRM is a fundamental model in quantum optics that describes the interaction between light and matter. It also serves as the theoretical basis for superconducting quantum bits, or qubits—the core components of quantum computers. Theoretical solutions for this model were found by Braak and others [1, 2], and their validity has been confirmed by experimental results.

On the other hand, the NCHO is a mathematical model introduced in 2002 by Parmeggiani and Wakayama [3, 4], driven purely by mathematical curiosity. It can be regarded as a generalization of the quantum harmonic oscillator, which itself models electromagnetic fields. The NCHO was proposed in order to reveal richer mathematical structures beyond those captured by conventional theories. Indeed, interesting phenomena from number theory and other areas of mathematics have been discovered in connection with the NCHO [5, 6].

Although the QRM and NCHO were originally introduced for entirely different purposes, previous studies ([7, 8]) revealed a surprising connection between them: by taking a certain limit of the NCHO, one can derive the (one-photon) QRM. However, these prior studies did not fully establish an explicit correspondence between the parameters of the NCHO (𝛼, 𝛽, 𝜆) and those of the QRM (𝑔, Δ, 𝜇)—see Figure 4. As a result, the theory lacked the concrete predictive power needed for practical applications.

Furthermore, while some researchers have pointed out various similarities between the NCHO and physical models, it remained unclear whether the NCHO itself directly corresponds to any physical system. A definitive physical interpretation had not been found.

Research Overview

This study [9, 10] led to two major findings, as illustrated in Figure 1:

Discovery 1:
We found that the NCHO, a mathematical model, is mathematically equivalent—as an eigenvalue problem—to the two-photon quantum Rabi model (2QRM)³, a physical model.

The 2QRM describes a system in which matter interacts simultaneously with two photons. This discovery reveals, for the first time, that the physical model corresponding to the NCHO is the 2QRM —something that had remained unclear until now.

Discovery 2:
We demonstrated, in a clear and explicit way, that taking an appropriate limit of the 2QRM yields the one-photon quantum Rabi model (1QRM).

This result refines the relationship between the NCHO and the 1QRM previously reported in earlier studies. In those prior works, the correspondence between the model parameters before and after taking the limit was not clearly established. Our study revisits this issue by viewing the connection instead as a limit transition from the two-photon to the one-photon QRM, and clarifies how the parameters correspond across this transition.

The NCHO has also been widely studied in number theory. With the current findings, this accumulated mathematical knowledge can now be brought to bear on quantum optics, potentially revealing new and mathematically intriguing properties of light-matter interaction models.

Thus, this research significantly deepens the collaboration between mathematics and physics. It also opens the door to a unified understanding of two fundamentally different models: 1QRM and 2QRM.

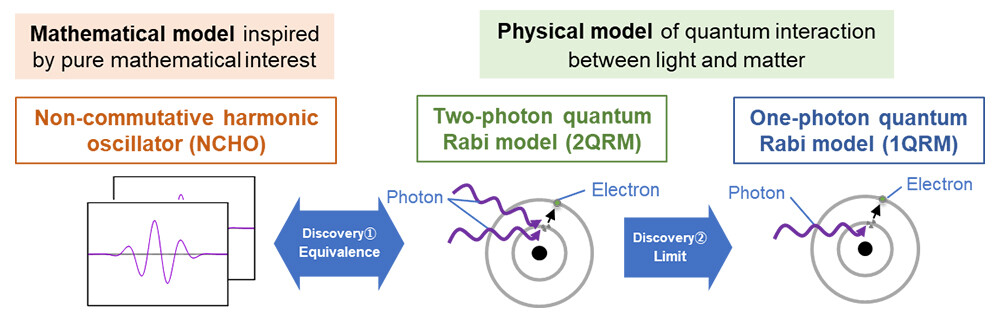Figure 1 Summary of Results

Technical Highlights

The key to this discovery lies in the innovative application of representation theory⁴, a core technique in fundamental mathematics. In particular, by focusing on the symmetries inherent in different mathematical spaces, we succeeded in proving the equivalence of the models by transforming the differential equations that describe them into new equations defined on alternative spaces with the same symmetry properties.

Figure 2 illustrates the flow of the proof. The research focuses on the linear space of all functions (not necessarily smooth) defined on the real line. By leveraging certain types of symmetry in this space, we establish the following identifications:

　Separately, using a different symmetry structure, we can identify:

The three models studied in this research are all formulated as systems of differential equations on the real line. Among them, the NCHO and the 2QRM yield solutions that can be decomposed into even and odd functions. Therefore, they are represented in the (B1) space and can be further transformed into differential equations defined on the (B2) space (see arrows a and b in Figures 2 and 3).

By rotating the complex disk (B2) by 90 degrees and appropriately substituting the NCHO parameters (𝛼, 𝛽, 𝜆) with those of the 2QRM (𝑔, Δ, 𝜇), we establish a correspondence between the two models as eigenvalue problems (arrow c). This proves Discovery 1: The equivalence of NCHO and 2QRM.

On the other hand, the 1QRM does not allow decomposition into even and odd functions, so it remains in the (A1) space. Its solutions can be transformed into those of a differential equation on the (A2) space (arrow d). Interestingly, the differential equations derived from transforming the 2QRM into the (B2) space can be generalized to disks of arbitrary radius. By treating the disk's radius as an additional parameter and taking the limit as the radius approaches infinity (arrow e), we obtain a differential equation on the (A2) space—which turns out to be equivalent to the transformed equation for 1QRM. This demonstrates Discovery 2: The 1QRM emerges as the limiting case of the 2QRM.

It is worth noting that the transformation of the 1QRM into a first-order system on the complex plane (arrow d) follows earlier works [1, 2, 7, 8], while the transformations represented by arrows (a), (b), (c), and (e) are newly developed in the present research.

Figure 2 The Structure of the Proof Organized in Terms of Function Spaces
Note. Discovery 1 corresponds to the arrows (a, c, b), and Discovery 2 corresponds to the arrows (b, e, d). In the previous studies⁵ [7, 8], the equivalence between the NCHO and the 2QRM was not discovered through the arrows (f, g, h, d).

Furthermore, the specific forms of the differential equations appearing at each step, as well as the parameter correspondences in steps (c) and (e), are illustrated in Figure 3.
　Here, we denote the radius of the disk by √𝜈 and treat 𝜈 as an additional parameter. (Some of the symbols are defined in Figure 4. Note that the definition of the 2QRM used in Figure 3 slightly differs from that in Figure 4, but they are equivalent if we replace 𝜇 by 𝜇+1/2.)

Figure 3 Structure of the Proof Focusing on the Correspondence Between Parameters
Note. The upper two rows represent Discovery 1, and the lower two rows represent Discovery 2. The labels on the arrows (a-e) correspond to those in Figure 2.

Future Outlook and Societal Significance

The QRM is regarded as a promising theoretical foundation for the basic components of quantum computers using superconducting circuits. Until now, the QRM and the NCHO have been studied independently in the fields of physics and mathematics, respectively. This research has revealed a connection between these two models.

By linking the previously separate lines of research, this discovery opens the door to new insights—such as exploring number-theoretic properties of the QRMs (both one-photon and two-photon variants). Moving forward, we aim to build on this result through collaboration within NTT's research laboratories, progressing step by step: predicting new phenomena through theory and validating them experimentally, in pursuit of deeper scientific truths.

In particular, while the 1QRM has already seen its theoretical predictions confirmed through experiments, the 2QRM has not yet undergone sufficient experimental verification. This study has clarified the mathematical connection between the 1QRM and 2QRM, thereby strengthening the case for investigating the physical implications of the two-photon model and promoting its experimental validation.

By accumulating such theoretical and experimental discoveries, this line of research holds promise for contributing to the eventual realization of practical quantum computing elements based on superconducting technology.

Glossary

¹Non-commutative Harmonic Oscillator
The non-commutative harmonic oscillator is a mathematical model introduced in 2002 by Parmeggiani and Wakayama [3, 4], originally from a purely mathematical interest. It extends the conventional quantum harmonic oscillator—which models a single-frequency quantum electromagnetic field—by incorporating non-commutativity (complexity), aiming to uncover richer mathematical structures than those arising under commutative (simpler) structures.
This model is described by a differential operator (Hamiltonian operator) involving two parameters (𝛼, 𝛽), as given in Equation (1-i) in Figure 4. Solving the model corresponds to finding all eigenvalues of this operator—that is, finding all values of 𝜆 such that there exists a square-integrable function 𝑓, defined over the real line, satisfying Equation (1-ii). In other words, for given (𝛼, 𝛽, 𝜆), the central question is whether a function 𝑓 exists that solves the equation.
This model has been actively studied from foundational mathematical perspectives, particularly in number theory. One notable example is the study of the "spectral zeta function," which is constructed from the set of all eigenvalues (eigenenergies) of the model and can be regarded as an extension of the Riemann zeta function. This connects to analytic number theory, especially the theory of modular forms [5, 6].
Now that a relationship between this mathematical model and a physical model has been uncovered, it has become an intriguing question to explore the physical implications of its foundational mathematical properties.

²(One-photon) Quantum Rabi Model
The quantum Rabi model is a fundamental model in quantum optics that describes the interaction between light and matter. It specifically models how a two-level atom (a simplified representation of matter) interacts with a single-frequency electromagnetic field, absorbing and emitting photons. Experimentally, this interaction is realized by confining photons in a resonator and coupling them with artificial two-level atoms.
Mathematically, the model is described by a differential operator (Hamiltonian operator) involving two parameters, (𝑔, Δ), as given in Equation (2-i) in Figure 4. Solving the model means determining all eigenvalues of this operator—that is, identifying all values of 𝜇 for which there exists a square-integrable function 𝑓, defined over the real line, that satisfies Equation (2-ii). In other words, the goal is to determine, for each set of values (𝑔, Δ, 𝜇), whether there exists a function 𝑓 that satisfies the equation.
For many years, it was believed that the eigenvalues (or eigenenergies) of the quantum Rabi model could not be computed explicitly. As a result, researchers often used an alternative, analytically solvable model—the Jaynes-Cummings model—based on the rotating wave approximation (RWA), in which all eigenvalues can be written out explicitly. However, with advances in experimental techniques, discrepancies between this approximation and experimental results began to surface.
This situation changed when Braak [1, 2] showed that the eigenvalues of the quantum Rabi model can, in fact, be calculated. Following this theoretical breakthrough, the model's validity has also been experimentally verified. Nonetheless, writing down all eigenvalues simultaneously in closed form remains difficult, and a complete understanding of the model has yet to be achieved.

³Two-Photon Quantum Rabi Model
The two-photon quantum Rabi model describes a nonlinear interaction in which matter simultaneously absorbs or emits two photons. This phenomenon is believed to occur at the focal point of laser light, and if its location can be controlled, it holds promise for applications such as high-resolution imaging. However, experimental verification of this phenomenon remains limited at present, making it an important subject for future investigation.

Figure 4 Equations Characterizing Each Model

⁴Representation theory
Representation theory is a field of fundamental mathematics that studies symmetries in linear spaces. Symmetries of ordinary shapes can be described as collections of transformations that leave the shapes unchanged. For example, the symmetries of a square can be represented by rotations of 0°, 90°, 180°, and 270°, as well as reflections across the vertical axis, horizontal axis, and the two diagonals. Generalizing this idea, one can formulate symmetries of more abstract spaces as collections of transformations that preserve certain structures of those spaces. Among such cases, representation theory focuses on the symmetries of linear spaces—spaces that allow addition and scalar multiplication and are thus particularly tractable.
Representation theory plays a vital role in many areas of physics, including quantum mechanics. In the present study, new insights were gained by using intertwining operators—maps that connect different spaces sharing the same symmetry, though they may appear different in form. These operators allowed for the transformation of differential equations describing one model into differential equations defined on another space.

⁵Comparison with previous studies
In the previous studies [7, 8], the method of transforming the 1QRM into a system of first-order differential equations on the complex plane—indicated by arrow (d) in Figure 2 (subsequent arrows are also indicated in the same figure)—is shared with the present work. In [7, 8], it was also shown, through heuristic arguments, that the non-commutative harmonic oscillator (NCHO) can be transformed into a second-order scalar differential equation on a certain complex domain (arrow (f)). Furthermore, by introducing an additional parameter to this equation and taking the limit as this parameter tends to infinity (arrow (g)), it was shown that the resulting equation converges to a second-order scalar differential equation obtained by transforming the 1QRM's system into a single higher-order equation (arrow (h)).
However, in [7, 8], the precise shape of the complex domain involved was not specified. Additionally, no explicit correspondence was provided between the parameters of the equations before and after the limit—namely, (𝛼, 𝛽, 𝜆) for the NCHO and (𝑔', Δ', 𝜇') for the transformed 1QRM.
In this study, we first present an explicit formulation of the correspondence previously proposed heuristically in arrow (f), by decomposing it into arrow (a) and the single-equation transformation. This reveals that the transformed complex domain is a disk, and the additional parameter can be interpreted as the radius of this disk. Moreover, by dividing the limiting process indicated by arrow (g) into two steps—arrows (c) and (e)—we clarify the correspondence between the parameters. Finally, by omitting the single-equation transformation step (arrow (h), which is also embedded in arrow (f)) and treating all equations as systems throughout, we are able to simplify the overall discussion.

References

^[1]D. Braak, "Integrability of the Rabi model." Physical Review Letters Vol. 107, 100401, pp. 4, 2011.

^[2]D. Braak, "A generalized G-function for the quantum Rabi model." Annalen der Physik Vol. 525, No. 3, pp. L23-L28, 2013.

^[3]A, Parmeggiani, M. Wakayama, "Non-commutative harmonic oscillators. I." Forum Mathematicum Vol. 14, No. 4, pp. 539-604, 2002.

^[4]A. Parmeggiani, M. Wakayama, "Non-commutative harmonic oscillators. II." Forum Mathematicum Vol. 14, No. 5, pp. 669-690, 2002.

^[5]T. Ichinose, M. Wakayama, "Zeta functions for the spectrum of the noncommutative harmonic oscillators." Communications in Mathematical Physics Vol. 258, No. 3, pp. 697-739, 2005.

^[6]K. Kimoto, M. Wakayama, "Apéry-like numbers for non-commutative harmonic oscillators and automorphic integrals." Annales de l'Institut Henri Poincaré D Vol. 10, No. 2, pp. 205-275, 2023.

^[7]C. Reyes-Bustos, M. Wakayama, "Covering families of the asymmetric quantum Rabi model: 𝜂-shifted non-commutative harmonic oscillators," Communications in Mathematical Physics Vol. 403, No. 3, pp. 1429-1476, 2023.

^[8]M. Wakayama, "Equivalence between the eigenvalue problem of non-commutative harmonic oscillators and existence of holomorphic solutions of Heun differential equations, eigenstates degeneration, and the Rabi model," International Mathematics Research Notices (IMRN), 2016, No. 3, pp. 759-94.

^[9]R. Nakahama, "Representation theory of sl(2,R)≃su(1,1) and a generalization of non-commutative harmonic oscillators," Mathematical Foundations for Post-Quantum Cryptography, Springer, pp. 20, 2025, in press, arXiv:2310.17118.

^[10]R. Nakahama, "Equivalence between non-commutative harmonic oscillators and two-photon quantum Rabi models", International Mathematics Research Notices (IMRN) 2025, No. 7, rnaf066, pp. 9, arXiv:2405.19814.

About NTT

NTT contributes to a sustainable society through the power of innovation. We are a leading global technology company providing services to consumers and businesses as a mobile operator, infrastructure, networks, applications, and consulting provider. Our offerings include digital business consulting, managed application services, workplace and cloud solutions, data center and edge computing, all supported by our deep global industry expertise. We are over $92B in revenue and 330,000 employees, with $3.6B in annual R&D investments. Our operations span across 80+ countries and regions, allowing us to serve clients in over 190 of them. We serve over 75% of Fortune Global 100 companies, thousands of other enterprise and government clients and millions of consumers.