量子的間接制御における数学的枠組の構築に世界で初めて成功
～量子情報処理のノイズ低減に向けた新たな指針として期待～

日本電信電話株式会社（本社：東京都千代田区、代表取締役社長：澤田　純、以下「NTT」）は、量子的間接制御※1において、直接操作が可能な量子系の自由度が極端に小さくても、間接的に繋がった量子系に対しての十分な制御性が普遍的に存在することを示しました。

本研究では、量子的間接制御の背後にある数学的に普遍な構造を明らかにしました。これまで、量子的間接制御は、様々な量子的間接制御それぞれに解析がなされ、個別にその性質が議論されていました。しかし、量子系の規模が増すと解析の困難さも増すため、量子計算機など、中規模以上の量子系においては、量子的間接制御は利用が困難であると考えられていました。本研究では、規模がいかに大きな量子系であろうとも、そこに含まれる２個以上の量子ビットを任意に操作できれば、その量子ビットに間接的に繋がった量子系に対する任意の制御が本質的には普遍的に可能であることが示されました。

これは、量子的間接制御が、中規模以上の量子系を用いた量子情報処理を実現する手段の一つとして候補になりうることを示唆します。

1．背景

近年、量子計算機をはじめとする量子情報処理に対して、その実現への期待が集まっています。しかし、現在実現している中規模以上の量子情報処理においては、システムに混入するノイズが大きく、多くの場合において量子的性質を有効に活用できるまでには至っていません。実現へ向けたノイズ低減のための現在の研究は、電磁遮蔽などの物理的手段によるノイズの遮断と、量子誤り訂正符号を用いた理論的なノイズの影響の排除が中心となっていますが、未だ十分なノイズ低減の実現は見通せていません。

その一方、1量子ビットの量子メモリーなど、小規模の量子情報処理においては、NVセンタ※2などを使った量子的間接制御のように、外部からのノイズなどの影響を原理的に受けにくい量子系を量子情報処理に利用する実験的な実証がNTT物性科学基礎研究所や他の研究機関でなされてきました。しかし、大規模な系での量子的間接制御は、その複雑性故に実現していませんでした。

2．研究の成果

NTTコミュニケーション科学基礎研究所は、量子的間接制御によって実現可能な制御の集合を完全に分類することで、量子的間接制御が持つ普遍的な性質を明らかにしました。例えば、直接操作可能な量子系が3次元※3以上の場合は、その量子系が繋がっている量子系全体を間接的にではあるが任意に制御可能な状況が確率的に混合した状態であると、必ず見なせることを明らかにしました。

これによって、次元が高い量子的間接制御においても、解析に対して見通しの良い視点が得られ、量子誤り訂正符号に加えたノイズ低減の手段として、量子情報処理への量子的間接制御の利用促進が期待されます。

3．技術のポイント

3-1．量子系への操作性とノイズ侵入の容易さ（図1）

一般的に、量子系の操作は、外部環境の人為的変更によって実現します。そのため、量子系を操作するためには外部環境の変化によって量子系の変化が応答して発生することが必要不可欠です。しかし、人為的な操作以外の影響でも外部環境は変化するため、外部環境への応答性はノイズ侵入の原因にもなります。そこで、量子情報処理を実現する手段として、適度な応答性を持つ量子系が利用されます。実際、応答性が低すぎる量子系では、ノイズの侵入が原理的に減少する代わりに、操作性も悪化します。つまり、量子系への操作の容易性とノイズ侵入の困難性との間にはトレードオフの関係が原理的に存在します。実際、現状の量子計算機においては、アルゴリズムに制限が加えられないよう、一定以上の操作性があることを前提としており、そのことがノイズ侵入を防ぐ上での原理的な限界を与えています。そのため、操作性が制限された中でも自由に全体制御が可能であることがわかれば、ノイズ低減を高いレベルで達成したうえで、制限のない量子情報処理を実現できることが期待されます。

3-2．制御設計の第一歩である動的Lie代数※4

量子系への可能な制御の集合は、動的Lie代数と呼ばれる歪エルミート行列※5の集合によって表現されることが知られています。量子系への何らかの制御の実現を考えるに際し、対応する動的Lie代数が何かを知ることがその第一歩となります。例えば、現在考えられている典型的な量子計算機のモデルにあるような高い操作性を実現している場合、対応する動的Lie代数は全ての歪エルミート行列を含むことがすでに知られています。

3-3．量子的間接制御における動的Lie代数の分類に成功

操作性が低い量子系の場合、それに対応する動的Lie代数には多様な可能性が存在します。それ故に、普遍的な性質を抽出することが困難でした。しかし、操作が量子的間接制御によって行われる場合、その動的Lie代数にはJordan代数※6と深く関連する構造が必ず存在することを発見しました。Jordan代数は動的Lie代数に比べて多様性が非常に小さいことが知られています。この発見を用いることで、量子的間接制御の場合の動的Lie代数を完全に分類するとともに、そこから普遍的な事実を抽出することに成功しました。

得られた結果によれば、どのような量子的間接制御であったとしても、適切な基底をとることで、動的Lie代数に含まれる任意の行列が同時ブロック対角化されると共に、各ブロック対角成分は同時に二つの空間の直積として記述されます。 ここで、直積の右側の空間への作用は直接操作可能な量子系へ影響を与えない作用であることが保証されます。（図2）

また、ブロック対角で記述できることは、確率的に混合した状態として認識できることを意味します。さらに、直接操作可能な量子系が3次元以上の場合、直積で定義される二つの空間のうちの左側の直接操作可能な量子系へ影響を与える空間に対する作用としては任意の歪エルミート行列が動的Lie代数に含まれることがわかります。このことが、任意の制御が実現できることを意味します。

3-4．動的Lie代数の構造と、直接制御可能な量子系の次元との関係

得られた量子的間接制御における動的Lie代数の分類を行うことで、直接操作可能な量子系の次元によって、動的Lie代数の構造が全く異なることがわかりました。特に、次元が3以上の場合は、量子的間接制御に対応する動的Lie代数は、影響を及ぼせる空間に対する全ての歪エルミート行列を必ず含みます。つまり、次元が3以上の場合には、実質的に背後にある量子系を任意に制御可能であることを意味しています。このことは、量子情報処理として制御の可・不可を議論する範囲においては、次元が3の量子系さえ操作できれば十分であることを意味しています。

4．今後の展開

量子的間接制御を実際に量子情報処理の実現手段として使えるように、理論を発展させます。現在の理論では制御の対象とする空間が有限次元（閉鎖系）の場合を仮定していますが、実際の量子情報処理を実現するためには、量子系は無限次元（開放系）であるとして扱わなければなりません。そこで、間接的にしか制御できない部分の量子系の次元が無限大の場合へ、理論を拡張することをめざします。また、本成果においては制御の可否のみを議論しており、現在の理論体系のままでは所望の制御実現に必要な時間を議論することはできませんでした。そこで、時間の観点をも含む理論へと発展させることで、より実用に耐えうる理論へと発展させます。さらに、少数量子ビット系において、本研究で構築した理論の実装を行い原理検証実験も行っていく予定です。

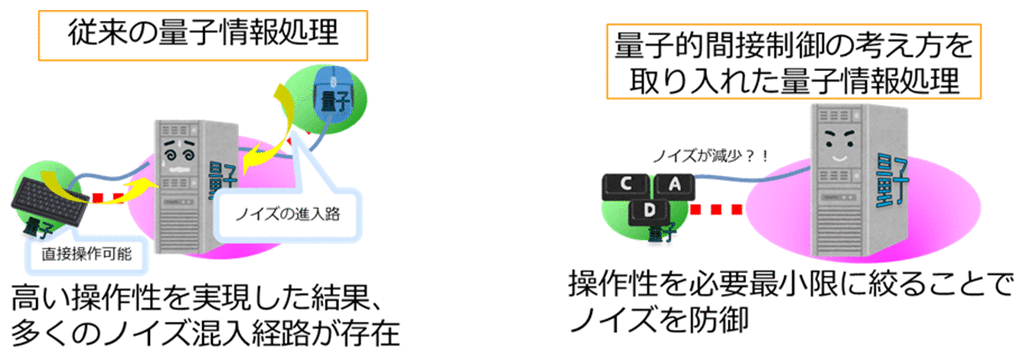図1：ノイズ対策の観点からみた量子的間接制御

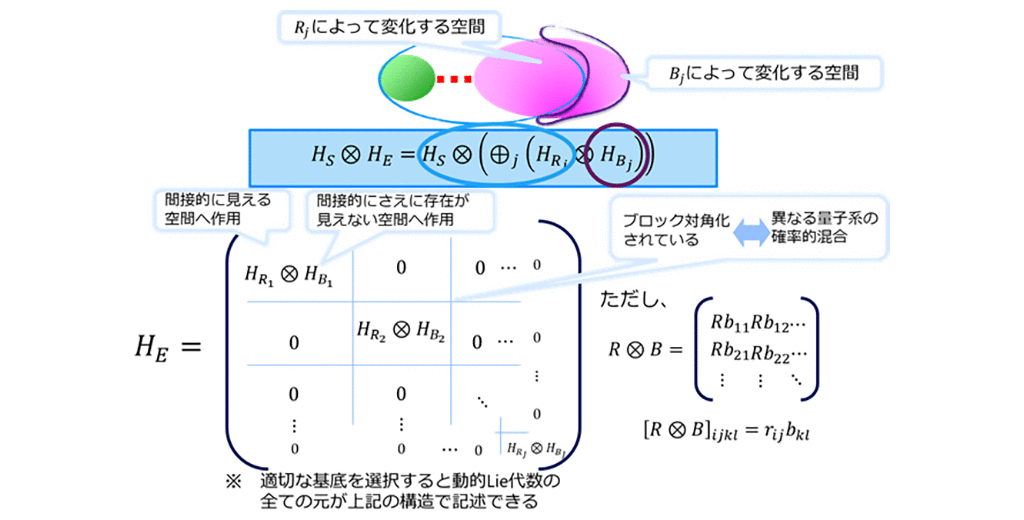図2：量子的間接制御において動的Lie代数が普遍的に持つ構造

用語解説

※1 量子的間接制御

二つの量子系において、片方の量子系のみへの操作と二つの量子系を繋げる自発的な相互作用とを利用することで二つの量子系全体を制御すること。

※2 NVセンタ

ダイヤモンド結晶中にある窒素-空孔よりなる欠陥。ノイズの影響を受けにくいとして、量子情報処理の手段として注目される量子系

※3 次元

通常の情報処理で言うところの基数。例えば3量子ビットからなる量子系は8次元である

※4 動的Lie代数

交換子積に関して閉じていて線形空間を成す元からなる集合。つまり、この集合の任意の二つの元をA,Bとし、任意の実数をx,yとすると、AB-BAやxA+yBもこの集合に含まれる。ここでは特に、歪エルミート行列からなる。数学的にはLie代数の一表現であるが、可能な量子制御の集合と一対一に対応するという物理的観点を強調するために、物理の分野では特にこのように呼ばれている。

※5 歪エルミート行列

複素共役+転置によって自身に負符号をつけたものになる行列。

※6 Jordan代数

反交換子積に対して閉じていて線形空間を成す元の集合。つまり、この集合の任意の二つの元をA,Bとし、任意の実数をx,yとすると、AB+BAやxA+yBもこの集合に含まれる。

研究協力の状況・関連文献

本成果は、大阪市立大学大学院理学研究科丸山客員教授・静岡大学情報学部情報科学科尾張准教授との共同研究の成果であり、JSPS科研費17K05591の助成を受けたものです。また、本成果の技術的内容は　Go Kato, Masaki Owari, Koji Maruyama "Algebra and Hilbert space structures induced by quantum probes," Ann. Phys. 412, 168046 (2020)　により発表されています。