2021年2月24日
日本電信電話株式会社
世界初、現実的な装置を用いた量子力学的に安全な高速乱数生成に成功
~量子乱数生成器の実応用に向けて大きく前進~
日本電信電話株式会社(本社:東京都千代田区、代表取締役社長:澤田 純、以下「NTT」)は、現実的な光学装置を使い、高い安全性を達成する高速な量子乱数生成器(以下QRNG※1)を世界で初めて実現しました。
QRNGは量子測定(※2)の確率的な性質を利用して真の乱数を作り出す装置です。この乱数はもし盗聴者が量子力学的に可能な方法で盗聴を試みたとしても、その予測不可能性を保証できるという意味で量子力学的に安全な乱数にすることが可能です。これまでの乱数生成レートの高いQRNGは、装置の特性を完全に把握する必要があったため、現実的な装置を使った場合でも安全な乱数を生成することが出来ませんでした。一方、現実的な装置を使ったより安全なQRNGも知られていますが、乱数生成のための十分な無作為性(※3)を蓄積するまでに長時間装置を動かす必要がありました。このため乱数生成を開始してから要求した乱数を実際に生成するまでに大きな遅延を生じていました。実際のアプリケーションへの応用では、低遅延で乱数生成レートが高くかつ安全性の高いQRNGが望まれます。今回の研究成果ではアメリカ国立標準技術研究所(National Institute of Standards and Technology、以下NIST)と共に、少ない実験データから効率的に乱数の保証を行う理論手法の開発と、タイムビン量子ビット(※4)と呼ばれる光パルスの到着時刻の測定を用いることで、0.1秒毎に8192ビットの量子力学的に安全な乱数を生成することに成功しました。本研究成果は、低遅延かつ高い乱数生成レートとともに、現実的な装置を使って安全な量子乱数生成器を実現するものです。
本研究成果は、英国科学誌Nature Communicationsに2月24日(現地時間)オンラインで掲載されました。
1.研究の背景
乱数生成器(以下RNG)は名前の通り乱数を作り出すための装置です。RNGの出力が予測不可能かつ一様に分布していれば、乱数であると言うことが出来ます。予測不可能であることは装置を動かす前にその出力が決められないことを保証するもので、一様であることはRNGの出力がすべて同じ確率で発生することを保証します。また場合によっては、乱数がプライベートでありRNGの正規の利用者のみ、その値を知ることが可能である必要があります。乱数は数多くの科学分野や実社会のアプリケーションで有用であり、数値計算、サンプリング、ゲームや暗号といった様々な分野で利用されています。このような応用で、乱数が持つべき性質のうちのいくつかを満たした一見ランダムな値を、コインフリップのような古典力学的な過程を用いて作ることも出来ます。しかし、全ての古典力学的な過程は本質的には決定論的な過程であり(※3)、真に予測不可能な乱数を生成することは出来ません。これに対し、QRNGは、量子力学を利用することで「真の乱数」の生成を可能とするものです。
QRNGには様々な手法があります。例えば、二準位系の量子状態である量子ビット(※5)をある基底での均一な重ね合わせ状態(※6)として用意し、その基底で状態を測定する(※2)ことで真の乱数を生成することが可能です。さらに古典力学的な手法とは異なり、量子力学的な手法では検証可能な物理的仮定を使い測定結果のみに基づいて、全ての性質が保証された真の乱数を作ることも可能です。こうした背景のもとにQRNGを実現する研究が世界的に広がっています。しかしこれまでのQRNGは、乱数ビットの生成率や生成までの遅延時間などの性能に課題のあるQRNGか、現実的な安全性を担保するための装置の条件として検証が難しい仮定を用いたQRNGのどちらかに限られていました(表1)。実際の応用では、ビット生成率や遅延性能が良く、同時に現実的な安全性も保証できるQRNGを考案することが重要です。今回の研究成果では、このような性質を満たした初のQRNGを報告しています。
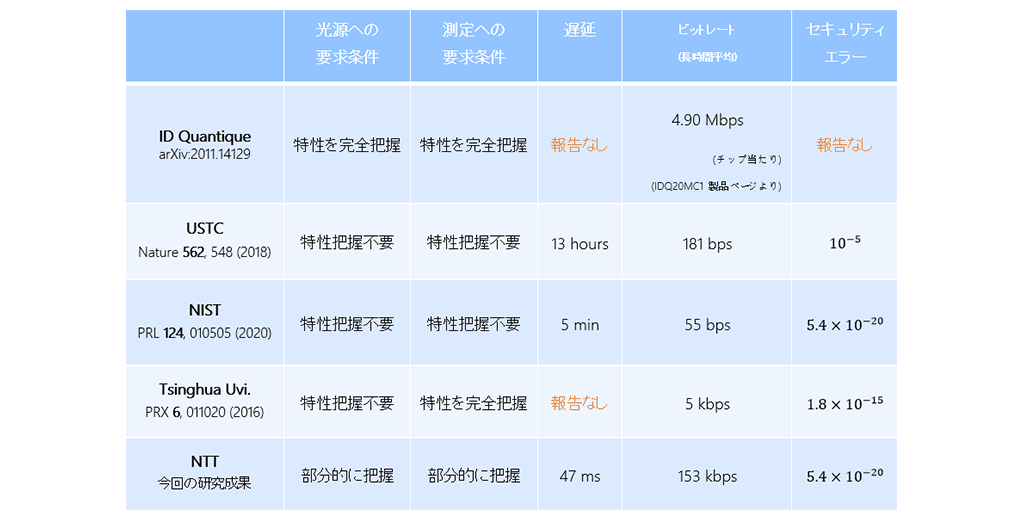 表1.これまでのQRNGの比較
表1.これまでのQRNGの比較
2.研究の成果
今回提案したQRNGの性能を検証するために、セキュリティエラー2-64≈5.4×10-20で量子力学的に安全性が保障された、8192ビットの乱数生成が要求される状況下での実験を行いました。理想的な場合QRNGは一様に分布し、かつ盗聴者に情報が漏れていない完全な乱数を生成します。しかし現実には生成された乱数は完全な乱数とは少し異なったものになります。セキュリティエラーとは、乱数生成要求時に設定するこの差に関するパラメータで、小さいほどより理想的かつ安全な乱数に近いことが保証できます。図1では、今回NTTが開発したQRNGが8192ビット以上の安全な乱数を、0.1秒ごとに抽出できることが示されており、想定した要求を満たすことに成功しています。
他の最先端のQRNGとの比較を表1に示します。このように、本QRNGは安全性と性能の両立を現実的な装置で実現しています。
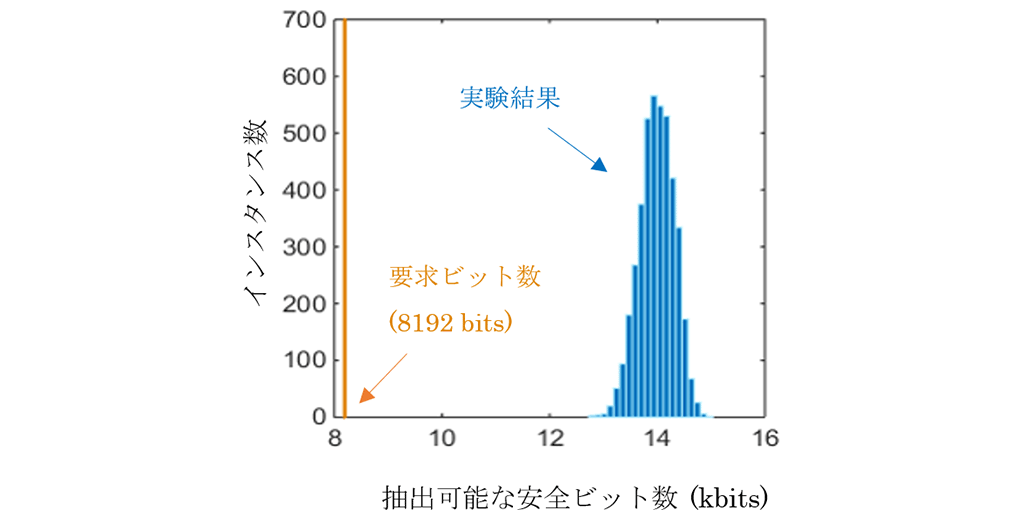 図1.今回のQRNGからセキュリティエラー2-64で抽出可能な安全ビット数のヒストグラム(4200インスタンス分) 。各インスタンスは0.1秒分の実験データを利用。
図1.今回のQRNGからセキュリティエラー2-64で抽出可能な安全ビット数のヒストグラム(4200インスタンス分) 。各インスタンスは0.1秒分の実験データを利用。
3.技術のポイント
1.光のタイムビン量子ビットを使ったシンプルな構成
タイムビン量子ビットは量子通信で広く利用されている光子(※7)の時刻に関する情報を使った安定した量子ビットです。二つの時刻を考え、そのどちらかの時刻に光子が存在する状態(図2上側)や、その両方に存在する重ね合わせ状態(図2下側)などを利用します。光子がある時刻に確定的に存在する状態に対して重ね合わせ状態への測定を行うと、不確定性原理により理想的にはその結果がランダムになります。安全な乱数を作るためには時刻が確定した状態と重ね合わせ状態の両方の測定が必要ですが、非対称マッハツェンダー干渉計(※8)と二つの単一光子検出器(※9)を使った構成を利用することで、これら2つの測定が同時に実装されたシンプルなQRNGを実現しています(図3)。
2.量子確率推定法による低遅延化と実用的な安全性保証
量子的な攻撃が可能な盗聴者に対する測定結果の無作為性は推定確率によって直接求められます。これは盗聴者が測定結果を正しく推定する最大の確率です。推定確率が高ければ、測定結果の無作為性は小さくなります。量子確率推定法は、この推定確率の上限を見積もる理論的な手法です。この手法では対象のQRNGの物理モデルを必要としますが、モデルに今回の実験における光源や測定装置の不完全性を部分的にうまく取り込むことで、現実的な装置を使ったQRNGの実用的な安全性を保証しています。また推定確率を他の既存手法より効率よく見積もることが出来るため、低遅延な乱数生成を可能にしています。
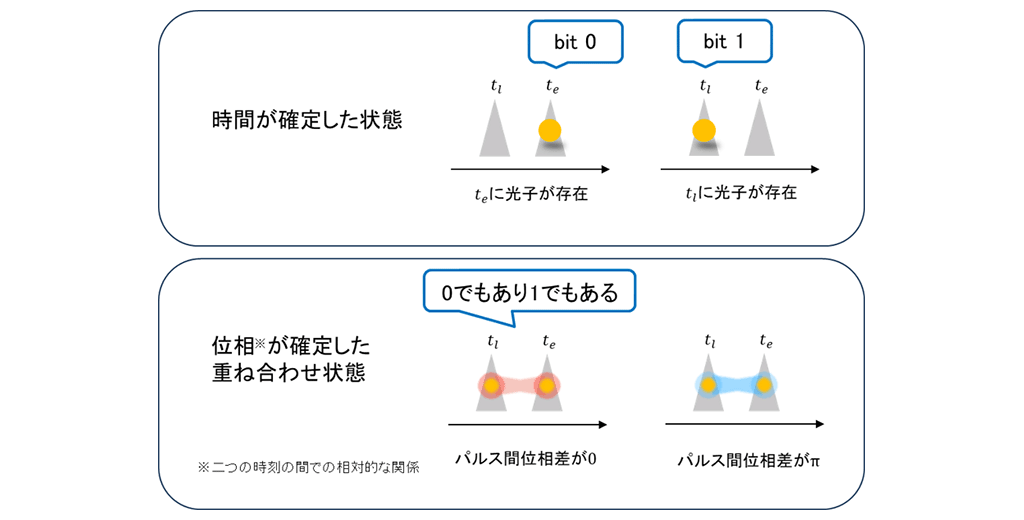 図2.タイムビン量子ビットを表す模式図
図2.タイムビン量子ビットを表す模式図
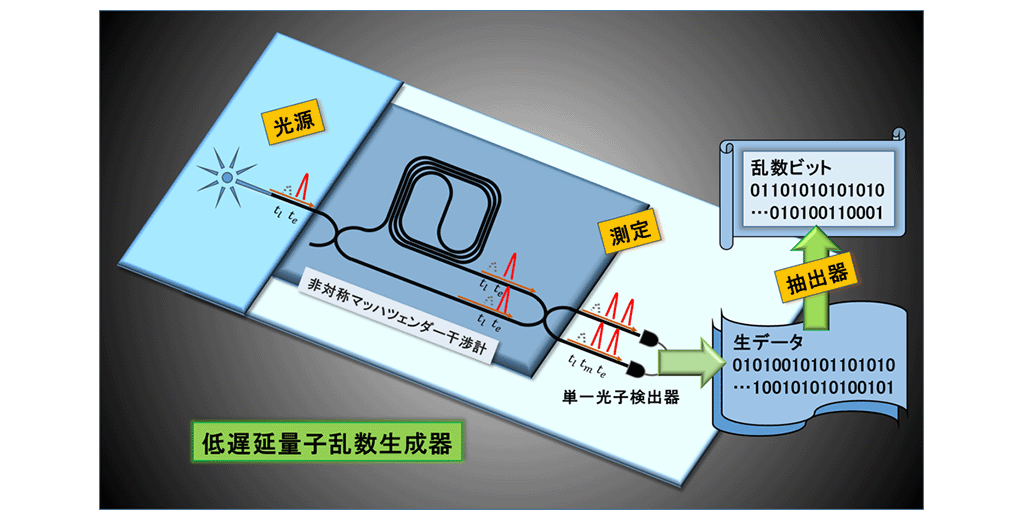 図3.NTTが開発したQRNGの概略図
図3.NTTが開発したQRNGの概略図
4.今後の展開
今回の研究で開発した低遅延で高い乱数生成レートのQRNGの展開として、高い安全性を保ちながら連続的に高速動作する量子乱数ビーコンの実現への応用が考えられます。量子乱数ビーコンとは一定の長さの安全性が保証された新しい乱数を繰り返し生成、公開するサーバーです。このような乱数はゼロ知識証明(※10)や選挙監査(※11)といった多くのアプリケーションに利用できます。別の展開としては今回開発したQRNGをコンパクト化するといったことが挙げられます。以上のような展開を通し、本成果が量子技術により安全性の飛躍的に向上した通信ネットワーク実現に寄与することが期待されます。
論文掲載情報
| タイトル | A simple low-latency real-time certifiable quantum random number generator |
|---|---|
| 著者 | Yanbao Zhang, Hsin-Pin Lo, Alan Mink, Takuya Ikuta, Toshimori Honjo, Hiroki Takesue, and William J. Munro | 掲載 | Nature Communications (2021). DOI: 10.1038/s41467-021-21069-8 |
| 発表日 | 24th Febuary 2021, London time (GMT) |
用語解説
※1量子乱数生成器
図4に示すように、一般的な量子乱数生成器はⅰ) 量子状態を用意するソース、ⅱ) 必要な測定を行う測定装置、ⅲ) 安全な乱数を抽出する抽出器の3つの要素から成り立っています。ⅰ), ⅱ)の要素は量子力学的な実験を行うことで実現されるため、量子的処理と呼ばれます。一方、ⅲ)の要素は古典的なプログラムを実行して実現されるため、古典的処理と呼ばれます。
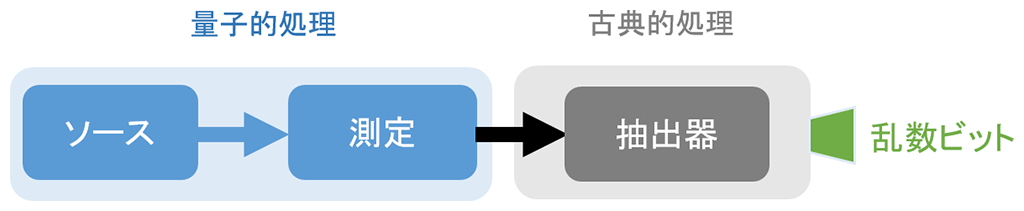 図4.一般的なQRNGの概略図
図4.一般的なQRNGの概略図
※2量子測定:
量子測定とは量子系の状態について知る手法のことです。量子状態はヒルベルト空間と呼ばれる状態空間上のベクトルとして見ることが出来ます。量子力学の重ね合わせの原理によれば、任意の量子状態はいくつかの明確に区別できる量子状態の和に分解して考えることが出来ます。この明確に区別できる状態のことを基底状態と呼びます。量子測定は量子状態をこれらの基底状態に射影するプロセスです。測定の後、量子状態はこれらの基底状態のどれかひとつの状態となりますが、その確率は元の量子状態と基底状態の重なりに応じた確率で決定されます。(厳密にはこれは射影測定と呼ばれるもので、この説明に当てはまらないような量子測定も存在します。)
※3無作為性:
無作為性は科学技術や実生活での重要な概念であり、また基本的なリソースでもあります。大まかにいえば、無作為性は対象となる系についての知識の欠落を表現していると言えますが、無作為性の厳密な定義は分野によって多少異なります。ここでは異なる目的にも合うよう、次のような操作的定義を考えています。もし事前知識があったとしてもその事象を正確に予測できなければ、その事象をランダムとし、そうでなければ決定論的とします。
※4タイムビン量子ビット:
タイムビン量子ビットは、二種類の時間位置に関する重ね合わせ状態を使った量子ビットです。タイムビン量子ビットによる実装は外部環境が量子状態に与える劣化に強く、単一光子を非対称マッハツェンダー干渉計に入力することで、状態を作ったり測定したりすることが出来ます。
※5量子ビット:
量子ビットは二準位の量子系のことで、量子情報における基本的な単位です。例えば、電子スピンのアップとダウンの二状態を使った量子ビットや、単一光子の偏波状態である垂直偏波と水平偏波を利用した量子ビットが挙げられます。古典力学的な系では、古典的なビットはどちらか一方の状態を取る必要があります。しかし量子力学においては両方の状態の重ね合わせ状態を取ることができ、これを量子力学や量子情報処理での基本的な特徴として利用することが出来ます。
※6重ね合わせ状態:
量子的な重ね合わせは量子力学の基本的な原理の一つです。古典的な波の振る舞いのように、あらゆる量子状態を足し合わせた状態もまた、量子力学的に許される状態であるという事を意味しています。これにより、明確に区別できる二つの状態に同時に存在し、測定するまでそのどちらにいるか決定することが出来ないような量子状態を取ることが可能になります。
※7単一光子:
単一光子は光の最も基本的な単位であり、量子化した電磁場としての素粒子としても知られています。
※8非対称マッハツェンダー干渉計:
非対称マッハツェンダー干渉計は光を二分岐した後に再び合波する光学装置です。分岐してからの光路長の違いにより合波時に光が干渉し、出力を強め合ったり弱めあったりする様子を観察できます。このような干渉を利用して、タイムビン量子ビットの重ね合わせ状態に関する測定を実装することが出来ます。
※9単一光子検出器:
光子が一つ以上あるかないかを検出できる特殊な光検出器で、光ファイバー通信、量子情報、天体物理学や物性科学といった様々な科学分野で利用されています。
※10ゼロ知識証明:
ゼロ知識証明は、自身の持っている秘密の情報そのものは他人に明かすことなく、その秘密を持っていることを証明する手法で、認証技術などに利用することが出来ます。認証システムでは、ユーザーとサーバーはお互いに他方を騙す不正がないようにする必要があります。このような不正回避に、公開された乱数が役立ちます。
※11選挙監査:
選挙監査は票が正しくカウントされていることや、適切な手続きが取られているといった事を投票終了後に確認するプロセスです。公平性と透明性を担保するためには、投票結果のサンプルをランダムかつおおやけに同意のとれた形で選ぶ必要があり、公開された乱数が必要になります。
本件に関する報道機関からのお問い合わせ先
日本電信電話株式会社
先端技術総合研究所 広報担当
science_coretech-pr-ml@hco.ntt.co.jp
TEL 046-240-5157
ニュースリリースに記載している情報は、発表日時点のものです。
現時点では、発表日時点での情報と異なる場合がありますので、あらかじめご了承いただくとともに、ご注意をお願いいたします。
NTT STORY
NTTとともに未来を考えるWEBメディアです。














