世界で初めての手法「超長方形分割」により、複雑なクラスタ構造の解析が可能に
～関係データ解析を行う機械学習に全く新しいパラダイムの提唱～

1．背景と歴史

長方形分割は、組合せ論、機械学習、確率・統計など、様々な学術分野に登場する重要な研究対象の一つです。長方形分割とは、長方形領域の分割で、分割された各ブロックが全て長方形となるもののことを指しています。長方形分割は興味深い様々な研究課題を提供し、例えば、ブロック数nの長方形分割は何通りあるのか、それらを列挙する効率的なアルゴリズムは存在するのか、またあらゆる長方形分割を表すことのできる確率モデルはどのように構成できるのかなど、多くの問題が研究されてきています。本成果では特に、近年の機械学習への活用として、関係データ解析への応用の観点からこの長方形分割に注目しています。
　関係データ解析は我々の普段の生活に広く普及している機械学習手法の一つで、ネットワークやグラフを含む関係データの中から何らかの構造を発見するための道具として幅広く利用されています。関係データ解析には膨大な方式がありますが、本研究では、その中でも特に結果の解釈のしやすさに長所を持つ方法として、長方形分割を用いた関係データ解析手法に注目しています。例えば図1（左）のように、入力データとして行方向にユーザ群、列方向に商品群を持つ行列型のデータを考えてみます。このとき、行列の各要素は、そのユーザがその商品を買ったか否かを二値（図1内の白黒）で表したものと捉えることができます。関係データ解析における典型的な応用として、あるユーザがある商品をどれくらいの確率で購買する可能性があるのか予測する問題が挙げられます。これは、観測行列データのある要素が白か黒かを当てる問題とも言い換えられます。一見すると、図1（左）の行列のある要素を予測するのは簡単でないように見えるかもしれません。ここで、関係データ行列の行と列を適切に並び替え、さらに長方形分割の補助線を与えることによって、図1（右）のように各ブロック内になるべく類似の要素が集まるように入力データを変換します。このようにすると、行列内の予測したい要素は、その要素が属するブロックの傾向（つまり、白ばかり集まるブロックなのか黒ばかり集まるブロックなのか）によって予測できるようになります。
　長方形分割を用いた関係データ解析の研究にも長い歴史があり、様々なモデルやその推論アルゴリズムが提案されています。それら様々な方法を特徴づける一つの重要な要素は、長方形分割を表すモデルの設計法の違いに起因しています。従来、様々な長方形分割モデルが提案され、近年の発展においては原理的にあらゆる長方形分割を表現しうるような極めて柔軟なモデルまでもが発見されてきました。しかし、それらのモデルを用いたデータ解析手法の実現には大きな困難が伴い、データによく適合する長方形分割を探索する問題は、計算機上取り扱いの難しい課題として今なお研究の発展途上にあります。そこで、長方形分割の探索問題を原理的に回避するような、新しいデータ解析パラダイムの創出が期待されてきました。

2．成果

本成果は、長方形分割を用いた関係データ解析において、従来ボトルネックとなってきた問題を原理的に回避する解析手法を実現したことにあります。長方形分割を用いた関係データ解析の具体的な問題は、図2（左）の通り、一般に入力の関係データに対して（1）行と列の並び替えを探す問題と（2）データによく適合する長方形分割を探す問題に帰着されます。従来、様々な長方形分割モデルが提案されてきましたが、いずれのモデル設計においてもデータ解析の段階において「（2）データによく適合する長方形分割を探す問題」がしばしばデータ解析手法の性能のボトルネックになっていました。本成果では、この関係データ解析問題において従来ボトルネックであった「（2）データによく適合する長方形分割を探す」処理を原理的に省略するデータ解析手法を創出しました。
　その実現の鍵となった原理は、図2（右）に示しますように、超長方形分割と呼ぶ極端に冗長な長方形分割モデルを導入したことにあります。この超長方形分割を用いることによって、提案するデータ解析アルゴリズムは、従来のボトルネックを回避し、結果としてベンチマークデータ課題において従来法と同等の計算速度と予測精度をより安定して（実験の複数回試行に対する低い標準偏差で）達成できました（表1）。これは、超長方形分割を用いた新しい機械学習パラダイムが、従来法とは別の原理に基づく別解となりえる可能性を示唆しています。

3．技術のポイント

本成果のポイントは、超長方形分割と呼ぶ対象を、長方形分割モデルの新たな概念として導入したことにあります。超長方形分割とは、図3のように自身の部分領域を切り出すことで、ありとあらゆる小さな（ブロック数の少ない）長方形分割を含むものを指しています。これは、極値組合せ論（※2）の世界で知られる超順列や超木と呼ばれる数学的対象（しばしば普遍対象（※3）とも呼ばれるもの）からの類推で生まれた新しい概念です。
　超長方形分割を長方形分割モデルとして用いることで、関係データ解析における（1）行と列の並び替えを探す問題と（2）データによく適合する長方形分割を探す問題の二つの問題は、「抽出する行と列の位置を超長方形分割から探す問題」の一つの形に帰着させることができます。これによって従来法のボトルネックであった「（2）データによく適合する長方形分割を探す問題」を回避し、データ解析自体が経験的に上手く機能することが確認できました。
　超長方形分割の構成法は、機械学習への応用を離れ、それ単独で数学的に非常に奥深い問題であり、本成果の中で解決していない未解決問題は、今後の研究の新しい展開となる可能性があります。超長方形分割の構成をめざすにあたって、本研究では二つの観察がありました。一つ目の観察は、組合せ論の世界で知られる事実として、全ての長方形分割は順列（自然数系列の並び替え）を介して表現できることに基づいています（図4）。この事実によって、長方形分割という幾何学的な対象は自然数の数列という代数的な対象を介して表せるようになります。二つ目の観察は、超長方形分割の同種の概念を順列において実現したものとして、超順列と呼ばれる対象の存在があることです。超順列はその部分系列としてあらゆる短い順列を含んでいることが知られています。これら二つの観察を基に、本成果では超長方形分割の有望な候補として、超順列に対応する極値的な長方形分割の候補としてジグザグ長方形分割と呼ぶ特別な長方形分割を創出しました（図5）。

4．将来の展望

普遍対象を用いた新しい機械学習パラダイムは、関係データ解析のみならず広範な機械学習課題に対して新たな戦略を与えることが期待されます。長方形分割問題のように、部分的に計算機上取り扱いの難しい問題が普遍対象を用いることで緩和される例は、他にも多くあるものと推測されます。機械学習のさらなる発展や自律した人工知能の実現に向け引き続き研究を推進して参ります。

発表・公開について

本成果は米国太平洋時間の3/28から開催される国際会議AISTATS （International Conference on Artificial Intelligence and Statistics） 2022 にて、下記のタイトル・著者で発表されます。

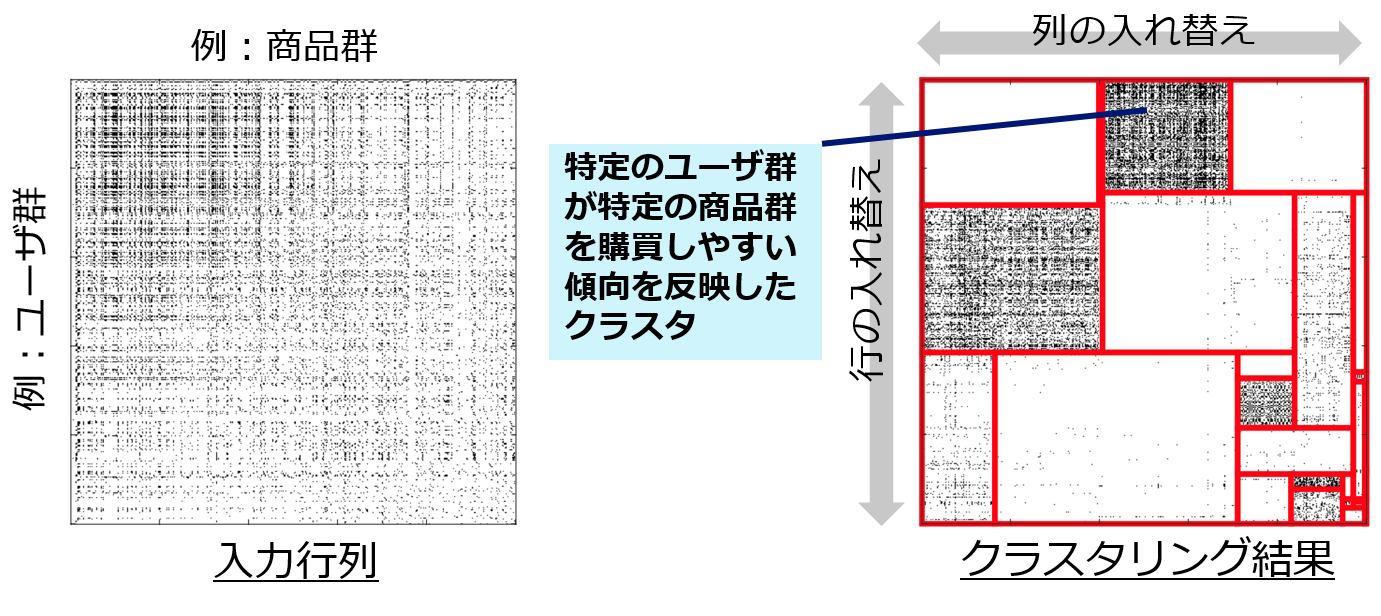図1：長方形分割による関係データ解析

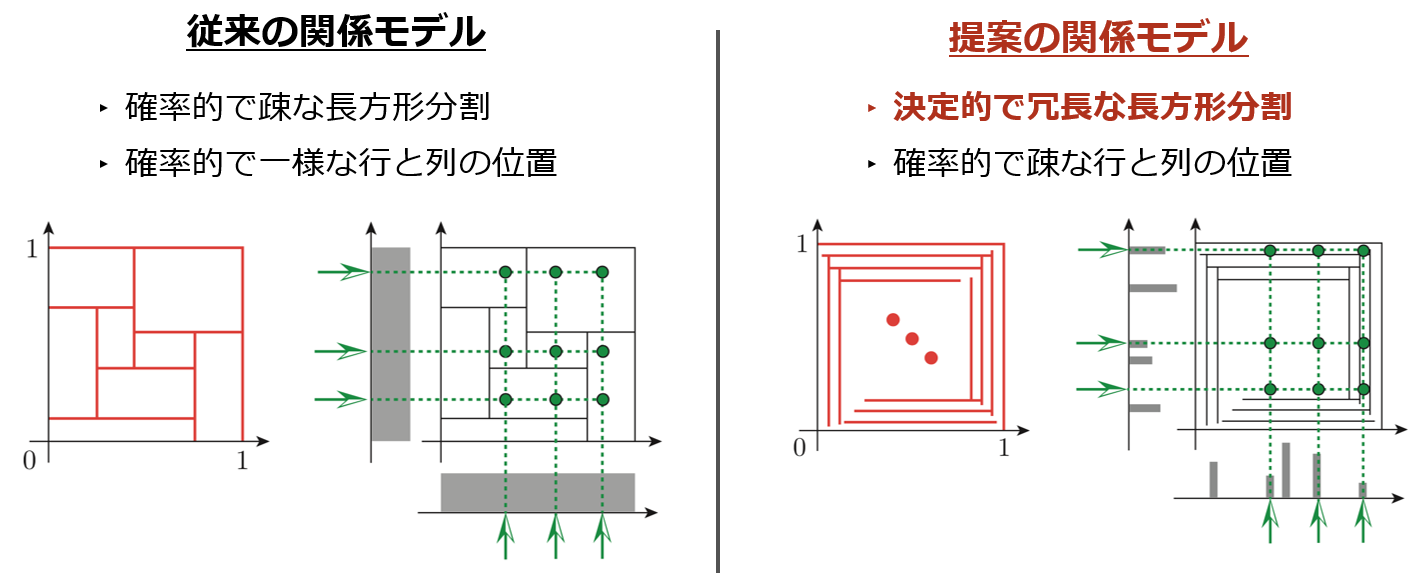図2： 関係データ解析モデルの従来法と提案法の比較概念図

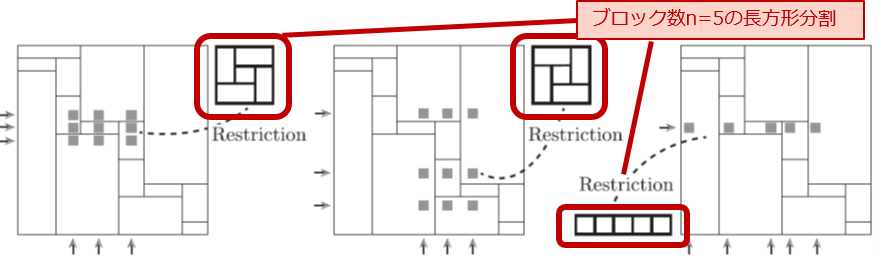図3： 超長方形分割の要件

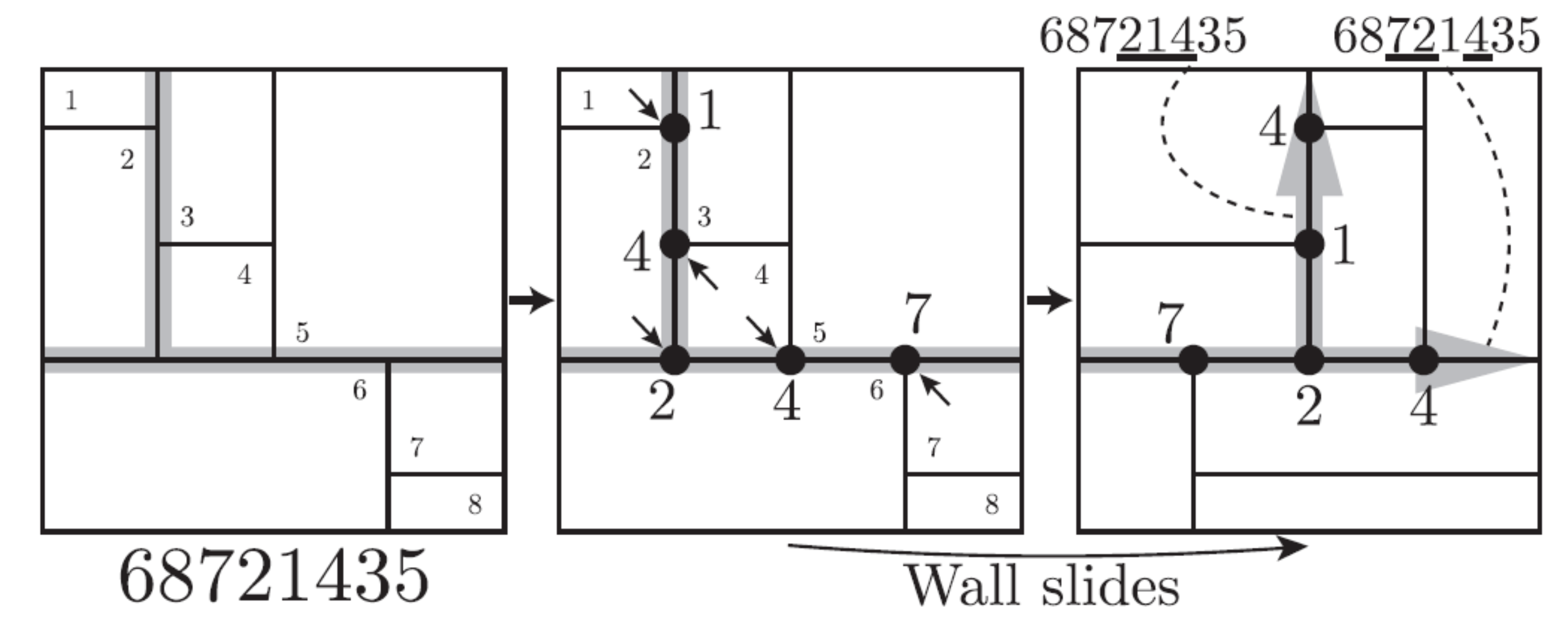図4： 順列から長方形分割への変換

図5：ジグザグ長方形分割

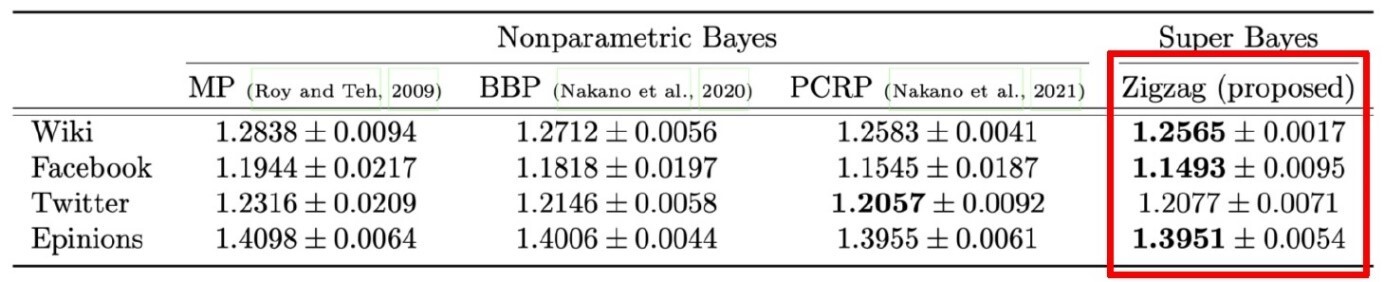表1：ベンチマーク結果
（行列のテスト用20%要素に対する各手法予測性能、10試行の平均・標準偏差であり、数値が小さいほど良い予測性能であることを示している。また標準偏差が小さいことは、悪い局所解に捕まりにくいことを表している）

用語解説

^※1Oral発表：
採録論文492件全てに与えられるposter発表に加え、一部の論文にはoral発表の追加の発表機会が与えられます。本成果はoral発表44件として採択されました。

^※2極値組合せ論
ある集合の部分集合を、様々な制約のもと最大で（または最小で）何個取ることが可能かを組合せ理論を用いて考察する理論です。

^※3普遍対象
ある集合の要素全てを自身の部分に内包するものを指します。典型的な例としては、ある長さ以下の全ての順列を部分系列として含む「超順列」や、あるサイズ以下の全ての木を部分木として含む「超木」などが研究対象となってきました。