MEMS集積化に向けた新しいカオス信号生成手法の実証に成功 ～機械学習などの信号処理技術への応用に期待～

日本電信電話株式会社（本社：東京都千代田区、代表取締役社長：澤田純、以下「NTT」）と国立大学法人 東京工業大学（本部：東京都目黒区、学長：益 一哉、以下「東工大」）科学技術創成研究院 Ludovico Minati特定准教授は共同で、従来手法よりも簡便で汎用性の高いカオス（※1）信号の生成手法を提案し、微細なメカニカル振動子（※2）を用いて動作実証することに世界で初めて成功しました。

昨今、機械学習や秘匿通信などの情報処理技術の分野において、カオス信号の活用が研究されています。携帯端末や医療応用においてその活用が盛んに進められているMEMS（Microelectromechanical Systems）の分野においても、制御性に優れ、集積化に適したカオス発生素子の研究が進められてきました。今回、メカニカル振動子が示す「秤動（※3）」を制御することにより、素子構造の微細化と低電圧駆動が可能な新しいカオス発生手法の実証に成功しました。この技術により、センサの入力情報を同じチップ上で機械学習させる半導体チップなど、新しいMEMS集積技術の発展が期待されます。

本成果は、NTTにおいて素子作製・測定を行い、東工大において理論計算に基づいたデータ解析を行うことによって得られたものであり、米国の科学誌「フィジカルレビューレターズ」（米国東部時間10月23日付）に掲載されました。

1.背景と成果の概要

カオスはさまざまな環境において共通に観測される物理現象で、一見無秩序に見える複雑な振る舞いでありながら、決まった法則に従って時間変化をするという規則性も有しています。近年、この複雑でありながら規則性を有するというカオスの特長を情報処理技術に用いようとする試みが進められており、リザバー計算などの機械学習（※4）や、秘匿通信、乱数発生などへの応用が広く研究されています。

一方、高感度センサや高周波フィルタ、プロジェクタなど様々な機器応用が行われているMEMSは、微細構造の機械的な「動き」を使って動作させる素子を、チップ上に集積化させたものです。このMEMSを用いたカオス発生手法の研究は、センサ部と信号処理部の集積化など、応用上の重要性にも関わらす、これまであまり進んでいませんでした。その大きな理由の一つは、MEMSを用いたカオス発生には櫛型電極などの複雑な素子構造が必要であり、また数十ボルトという高電圧が不可欠であったことにあります。

今回、メカニカル振動子の「秤動」運動に着目し、二つの異なる高周波信号を入力するだけという、極めて簡便な方法でカオス信号を発生させる手法を実証し、素子の小型化と低電圧駆動を実現しました。

2.実験の概要

作製した振動子（図1）は両持ち梁（※5）と呼ばれる架橋構造を有し、圧電半導体を微細加工することにより作製しました。電極に交流電圧を加えることにより、圧電効果を用いて構造を振動させることが可能です。今回、二つの異なる周波数の交流電圧を同時に加え、その周波数差を振動子の「秤動」運動に共鳴させるという新しい手法により、カオス的な振る舞いを示す複雑な信号の発生に成功し（図2）、得られた信号が実際にカオスの特徴を持つことが数値解析により確認されました。素子に加えた電圧は1～3ボルトと従来に比較して一桁程度小さな値であり、また両持ち梁という極めてシンプルな構造により、カオス信号の発生に成功しました。

3.技術のポイント

4.今後の展開

実験に用いた振動子の振動数は、まだ数メガヘルツという低い周波数であり、様々な応用に適用するには不十分です。より高周波のメカニカル振動子によるカオス発生の実現をめざします。また、実際にリザバー計算などの手法に適用し、カオス振動の有用性を実証していきます。

論文情報

"A Generic Rotating-Frame-Based Approach to Chaos Generation in Nonlinear M/NEMS Resonators",
S. Houri, M. Asano, H. Yamaguchi, N. Yoshimura, Y. Koike, and L. Minati
Physical Review Letters, 125, (2020)

用語解説

※1 カオス

生物の増殖や水の乱流、電気回路やレーザ光など、非線形性を持つ多くの環境で観測される物理現象で、一見無秩序に見える複雑な振る舞いでありながら、完全にランダムな振る舞いを示すノイズとは異なり、同じ初期条件で同じ振る舞いを示すという規則性を有するものです。同じ運動を繰り返さない「非周期性」や、ほんの少しの初期条件の違いが大きな変化を引き起こす「バタフライ効果」などの特徴を持ち、昨今ではリザバー計算などの機械学習や疑似乱数の発生、秘匿通信などの情報処理応用が検討されています。

※2 メカニカル振動子（機械振動子）

弾性変形を周期的に繰り返すことにより機械的な振動が継続する人工構造体。鐘や鉄琴など楽器の振動板もメカニカル振動子の一種です。最近では微細加工技術の発展にともない、髪の毛よりも小さなメカニカル振動子を半導体チップに集積することも可能になっており、MEMS振動子として実用化が進められています。メカニカル振動子の最も代表的な形状のひとつは本研究でも用いられている両持ち梁と呼ばれるもので、橋や鉄琴の振動板に類似した形状をしています。

※3 秤動

月や地球などの天体は自転や公転という決まった周期運動を行っていますが、この運動とともに、ゆっくりとした別の周期運動も行っています。このような運動は「秤動」と呼ばれ、自転や公転に比較して小さく、また周期も数年から数万年という大きなものであり、潮の満ち引きや他の惑星の引力など、様々な要因により引き起こされます。メカニカル振動子はある決まった周波数で規則的な振動運動を行いますが、振動子が持つ非線形性により完全な周期運動にはならず、長い周期の振幅変化を伴います。この振幅変化は天体の秤動運動に相当するものと言えますが、通常は天体と同様に非常に小さな変化しか見られません。しかし、秤動運動の周波数に相当する周期的な外力が加わると、共鳴現象により大きな秤動運動が引き起こされます。今回の研究では、外部より二つの振動数を加え、その差周波を秤動運動に共鳴させることにより、カオス信号を発生させることに成功しました。

※4 リザバー計算などの機械学習

機械学習とは人工知能を構成する技術の一つです。コンピュータにより大規模データから共通のパターンやルールを見つけ出し、それを新しい入力データに適用することにより、様々な判断や結果の予測を可能とする技術です。機械学習にも様々な手法が存在しますが、データ処理を行う非線形ネットワーク自体を学習させるディープラーニングなどの手法とは異なり、固定された非線形ネットワークからの出力の重みづけだけを学習させることにより機械学習を実現するリザバー計算の手法が、最近注目を集めています。リザバー計算ではカオス信号を用いることによりエラー率の優れた計算ができる可能性が指摘されています。

※5 両持ち梁

微細加工技術により作製されるメカニカル振動子の代表的な構造のひとつ。両側が固定された板バネ構造からなり、鉄琴の振動板のように弾性的な上下運動が振動を引き起こします。両側が固定されているため、振動により全体の長さが伸びて張力が発生します。この張力により共振周波数が高くなり、非線形性が生じます。

※6 非線形性

両持ち梁などのメカニカル振動子は、一般にフックの法則として知られている構造の弾性的な振る舞いを使っています。フックの法則が成立している材料では、構造に加わる力がその変形の大きさに比例します。このような振動子を線形振動子と呼びますが、振動子の構造によっては変形の大きさの2乗や3乗に比例した力も加わることがあります。このような振動子を非線形振動子と呼びます。今回用いた両持ち梁構造では、梁の両側が固定されていることにより振動振幅が大きくなると梁に沿った張力が発生しますが、この張力は変形の大きさの3乗に比例する力を引き起こします。今回の実験では、この非線形性を用いることによってカオスを発生させることに成功しました。

※7 圧電効果

物体に電圧を加えると、膨張したり収縮したりする現象のことを圧電効果と呼びます。この膨張・収縮により物体に作用する力を電気的に引き起こすことが可能です。また、逆の効果を用いることにより、振動を電気的に検出することも可能です。

※8 単結晶ヘテロ構造

異なる材料からなる薄膜を、単結晶性を維持したまま接合した構造です。分子線エピタキシ法や化学気相成長法などの結晶成長法を用いて作製されます。メカニカル振動子に用いた場合、高い結晶性により安定した振動特性が期待されます。また、材料の化学反応特性の相違を用い、両持ち梁のような架橋構造を容易に作製することができるというメリットもあります。

図1　実験に用いたメカニカル振動子と測定手法

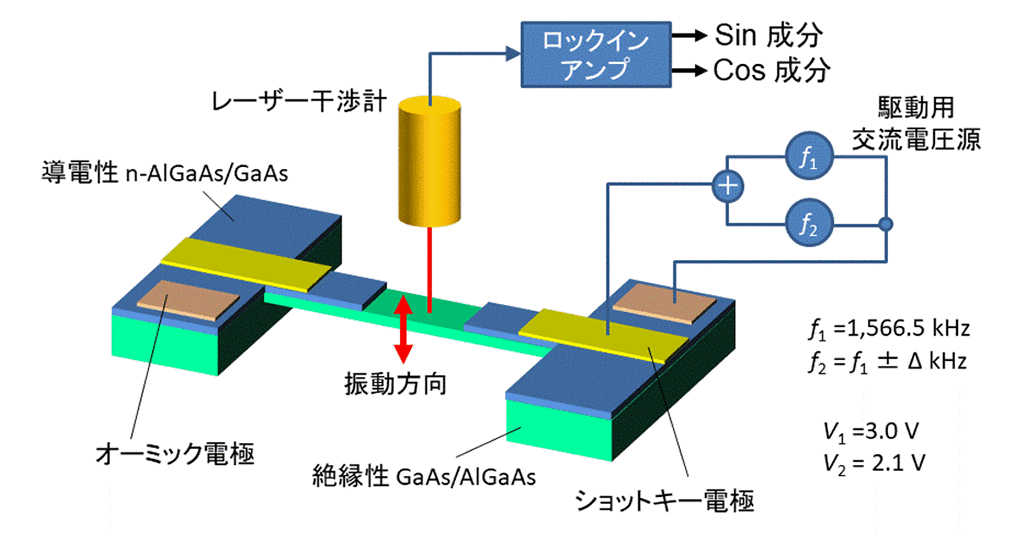図1　実験に用いたメカニカル振動子と測定手法の模式図。両持ち梁と呼ばれる架橋構造をGaAsとAlGaAsのヘテロ構造から作製しました。梁構造の長さは150ミクロン、幅は20ミクロン、厚さは0.6ミクロンです。構造の表面には振動の電気的な駆動と検出が可能となる電極が形成され、これらの電極にf1およびf2の二つの周波数の交流電圧を加えることにより、カオス的な振動状態を発生させます。振動の様子はレーザ干渉計で検出し、ロックインアンプを用いて振動のsin成分とcos成分を個別に測定することによって、カオスであることを確認します。

図2　測定された振動振幅変化の差周波数依存性

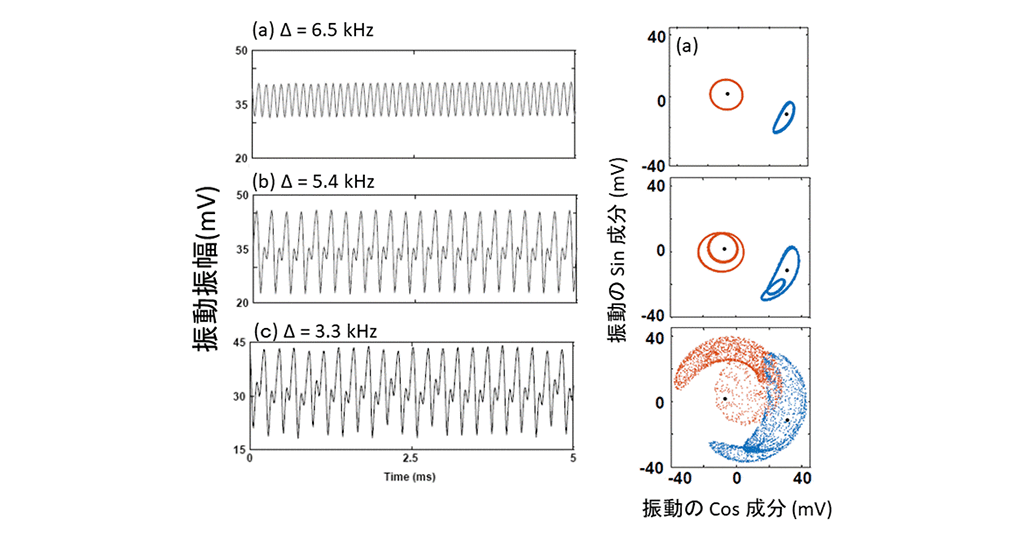図2　加えた二つの交流電圧の周波数差を変化させたときの、振動振幅の様子。(a) 周波数差が大きく、単調な秤動が引き起こされている場合。単一周期の秤動振動であるため、振動振幅は一定の周波数で変化しており、sin成分とcos成分も単純なループ状の軌跡を示す。(b) 周波数差が小さくなり、カオス振動の前段階である倍の周波数成分が発生。sin成分とcos成分の軌跡も、倍の周波数成分を反映し、2重のループになっている。(c)周波数差が秤動振動の共振を示した場合。振動の位相と振幅がランダムに変化するカオス的な秤動振動が観測された。sin成分とcos成分の軌跡も周期性のない複雑な振る舞いを示す。