世界初、分数電荷準粒子のアンドレーエフ反射の観測に成功
～超伝導特有の現象と考えられていた常識を覆す成果～

【概要】

日本電信電話株式会社（NTT）と科学技術振興機構（JST）は、フランス国立科学研究センター エクス=マルセイユ大学と共同で、半導体を用いて電子1個よりも小さな電荷（分数電荷準粒子^※１）のアンドレーエフ反射^※２を観測することに成功しました。これは二次元電子系^※３が低温・強磁場中で示す分数量子ホール状態^※４において、分数電荷準粒子が界面に入射する際、電子が透過し、分数電荷を持つ正孔が反射される現象です。これまでアンドレーエフ反射は超伝導体に特有の現象と考えられてきました。超伝導体では２つの電子がペア（クーパーペア）を作って電流を運ぶため、電子が超伝導体に入射する際、電子のペアが透過し、電荷を保存するように正孔が反射されます。超伝導体以外の物質におけるアンドレーエフ反射の可能性は1990年代に理論的に指摘されていましたが、理想的な界面を作ることが難しく、実験では観測されていませんでした。今回の実験により、半導体において、かつ分数電荷でもアンドレーエフ反射が起こることが明らかになり、現象の普遍性が示されました。分数電荷準粒子はトポロジカル量子計算^※５への応用も期待されています。本成果は、分数量子ホール状態と通常伝導体の界面における電荷移動メカニズムを明らかにするもので、準粒子を操作する量子情報デバイスの実現に向けて重要な知見を与えるものです。
　本研究は、5月14日英国科学誌 Nature Communications にオンラインで掲載されます。

１．研究の背景

超伝導体では２つの電子がペア（クーパーペア）を作って超伝導電流として流れます。超伝導体に外から電子（負の電荷e^※６を持つ。）が入射すると、この電子がクーパーペア（電荷2e）を作って超伝導体中に流れ込み、電流が増大します。一方、この過程全体では電荷量が保存する（電荷保存則^※７）ため、透過電流の増大を補償するために界面から正孔が反射されます（図１）。この一連の現象をアンドレーエフ反射と呼びます。アンドレーエフ反射は超伝導体界面における電荷移動の素過程^※８であり、超伝導接合を用いた様々なデバイスにおける基本原理です。
　従来、アンドレーエフ反射は超伝導体に特有の現象と考えられてきました。しかし、その根底にあるのは、より広い普遍性を持つ電荷保存則です。従って、電流を運ぶ粒子の電荷が電子の電荷eと異なれば、超伝導体以外でも同様の現象が起こる可能性があります。そのような系の代表として知られているのが、分数量子ホール系です。分数量子ホール効果は、二次元電子系に低温で垂直に強い磁場を加えたとき、ホール抵抗が特定の分数比を持つ値に量子化する現象であり、このとき電流を運ぶのは電子よりも小さな電荷（例えばe/3やe/5）を持つ分数電荷準粒子（以下、「準粒子」）です。いま、分数量子ホール系が通常の金属と接していて、準粒子が分数量子ホール系側から入射する場合を考えます。準粒子は金属の中に電子として入っていくため、界面で透過電流が増大し、同時にそれを補うべく準正孔の反射が起きて逆符号の反射電流が観測されると考えられます（図１）。この現象の観測は、アンドレーエフ反射が異なる物質同士の界面における普遍的な電荷移動メカニズムであることを確認することに等しく、物性物理学の極めて重要な課題であったと言えます。ところが1990年代にこの現象が理論的に予言されて以降、盛んに研究されてきたにもかかわらず、分数量子ホール系と金属の良質な界面を作製することが困難なため、今日に至るまで20年以上観測に成功した例はありませんでした。さらに、ある種の準粒子はトポロジカル量子計算における量子ビットの構成要素として期待されており、量子情報技術の発展のためにも、準粒子の基本的ダイナミクスであるアンドレーエフ反射の観測は大きな実験的課題であったと言えます。
　今回、研究チームは、ナノスケールの精密な半導体加工技術を駆使し、精密な分数-整数量子ホール接合^※９を作製することで、世界に先駆けて準粒子のアンドレーエフ反射の観測に成功しました。

２．研究の成果

実験では、まずGaAs半導体ヘテロ構造中の二次元電子系に低温で垂直磁場を印加し、電子系全体がランダウ準位占有率^※101の整数量子ホール状態になるように磁場の強さを調整しました。この状態で電子系の左側半分を覆う表面ゲート電極１にゲート電圧１を印加し、直下の電子密度を減少させて、ランダウ準位占有率1/3の分数量子ホール状態（図２の赤色領域、e/3の電荷を持つ準粒子によって電流が運ばれる状態）としました。このとき、試料の内部で分数量子ホール状態と整数量子ホール状態（青色領域、電子によって電流が運ばれる状態）の界面が形成されます。さらに、２つの領域の間にある微細ゲート２に負のゲート電圧２を印加し、その直下を空乏化することで、界面を1μm以下に狭窄して、微小な分数-整数量子ホール接合を実現しました（図２）。測定ではこの接合に分数側から電流を入力し、整数側に流れ出る透過電流を測定しました。すると、ゲート電圧２の値によって（接合の幅を変えることに相当）、入力した電流よりも大きな透過電流が観測される場合があることが分かりました（図３）。またこのとき、接合から分数側に返ってくる反射電流を測定すると、入力したものと逆符号の電流が観測されました（図３）。これら透過電流の増大、および負の反射電流は、分数電荷のアンドレーエフ反射が生じていることを示しています。この成果は、アンドレーエフ反射が超伝導特有の現象ではなく、普遍的なものであるということを示したもので、物性物理学の重要な成果だと言えます。

３．技術のポイント

ゲート電圧１（電極１）による電子密度制御によって、１つの半導体試料内に２つの異なる量子ホール状態（ランダウ準位占有率1/3領域、および1領域）を発現させました（図２）。この界面をゲート電圧２（電極２）によって狭窄することで、微小な分数-整数量子ホール接合を形成しました。この試料では、別々の材料をつなぎ合わせて作製する接合と比べ、格段に良質（不純物などの不確定要素が少ない）、かつ微小な分数量子ホール系の界面を実現することができます。加えて、ゲート電圧２によって狭窄領域の幅を調整することで、界面のサイズを精密に制御することにも成功しました。このような制御性の高い、良質かつ微小な接合により、準粒子のアンドレーエフ反射の観測が可能になりました。

４．今後の展開

超伝導体におけるアンドレーエフ反射は、超伝導接合を用いた様々なデバイスの基本原理です。今回の準粒子のアンドレーエフ反射も、今後その制御方法を改良していくことにより、様々な新機能を有する分数量子ホール効果デバイスに応用できる可能性があります。
　さらに今回、同一界面においてアンドレーエフ反射が繰り返し起こることで、準粒子と電子が一体となって運動し、一次元の伝導チャネルを形成することが分かりました。一次元チャネルは準粒子の導波路とみなすことができ、トポロジカル量子計算における信号伝送路としての利用が期待されています。今回の結果は一次元チャネル形成のメカニズムの１つを明らかにしたもので、量子信号伝送路の設計に向けて前進をもたらす成果だと言えます。

５．謝辞

本研究は、科学研究費補助金（JP16H06009, JP15H05854, JP26247051, JP19H05603）、および科学技術振興機構（JST）さきがけ（JP17940407）の支援を受けて行われました。

６．論文情報

掲載誌：Nature Communications

論文タイトル："Andreev reflection of fractional quantum Hall quasiparticles"

著者：Masayuki Hashisaka, Thibaut Jonckheere, Takafumi Akiho, Satoshi Sasaki, Jerome Rech, Thierry Martin, and Koji Muraki

DOI：10.1038/s41467-021-23160-6

７．用語説明

^※１分数電荷準粒子
分数量子ホール系において生じる電荷密度の変化の最小単位。電子よりも小さな分数電荷（今回の実験ではe/3）を持つ。分数量子ホール系^※４では、電子ではなく分数電荷準粒子が電流を運ぶ。ある種の分数量子ホール系の準粒子は、トポロジカル量子計算^※５の量子ビットの構成要素として期待されている。

^※２アンドレーエフ反射
電流は電荷を持つ粒子（キャリア）の流れである。通常の金属ではキャリアは電子（負の電荷 e^※６ を持つ）であるが、超伝導体では電子のペア（クーパーペア：電荷2e）、分数量子ホール系では準粒子（分数電荷：e/3など）がキャリアとなる。電子が超伝導体に入射するとき、クーパーペアを作って透過電流が増大し、電流を保存するように正孔が反射される。この現象をアンドレーエフ反射と呼ぶ。

^※３二次元電子系
平面状に電子が閉じ込められた系。半導体ヘテロ構造の界面や、グラフェンなどの原子層物質などで実現される。

^※４量子ホール状態
二次元電子系に低温で垂直に強い磁場を印加することで、ホール伝導度がe²/hを単位とする整数値（整数量子ホール効果）、または分数値（分数量子ホール効果）に量子化した電子状態（hはプランク定数）。量子ホール状態にある電子系の端には、一方向に電流が流れる一次元チャネル（エッジチャネル）が形成される。

^※５トポロジカル量子計算
物質の性質は「穴の数」のように安定的に飛び飛びの整数値をとる場合があり、このような性質を持つ物質をトポロジカル物質と呼ぶ。量子ホール効果のホール伝導度の量子化もトポロジカルな性質である。トポロジカル物質では、粒子の交換によって量子力学的状態を表現できる場合があり、この性質を利用して量子コンピュータ（トポロジカル量子コンピュータ）を実現できると予言されている。トポロジカル量子計算は他と比較してノイズ耐性が高く、エラー訂正不要な量子コンピュータを実現できると期待されており、世界中で活発な研究競争が行われている。

^※６負の電荷e
電子１個が持つ電荷（e = -1.602×10^-19 C）。その絶対値|e|は素電荷と呼ばれ、単独で取り出すことができる電気量の最小単位であり、陽子１個が持つ電荷に等しい。

^※７電荷保存則
物理現象の前後で電荷の総量が変化しないという自然界の基本法則。

^※８素過程
物理現象を構成する基本プロセス。複雑な現象は、素過程の組み合わせとして表現される。

^※９分数-整数量子ホール接合
分数量子ホール系と整数量子ホール系をつなぎ合わせた接合。前者では分数電荷準粒子、後者では電子が電流を運ぶことから、準粒子のアンドレーエフ反射が起こる。

^※１０ランダウ準位占有率
磁場（磁束密度）に対する電子密度の比。この値が整数値に近づくと整数量子ホール効果が生じ、特定の分数値（1/3など）に近づくと分数量子ホール効果が生じる。

８．図

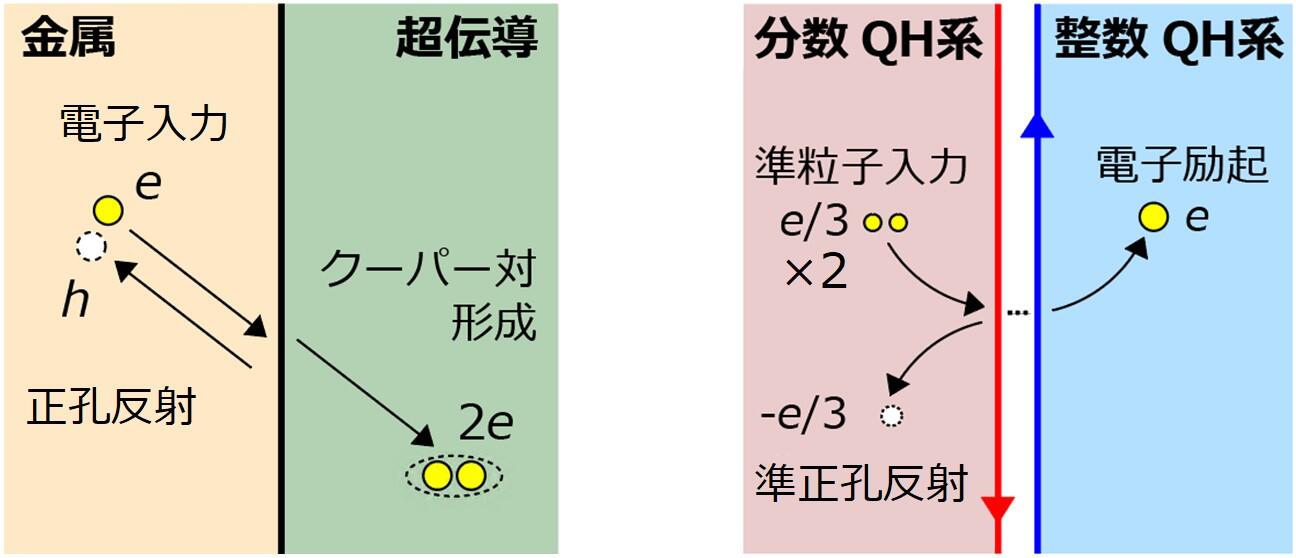図１：アンドレーエフ反射の概念図

左：従来の超伝導体接合におけるアンドレーエフ反射
右：分数－整数量子ホール（QH）接合における準粒子のアンドレーエフ反射

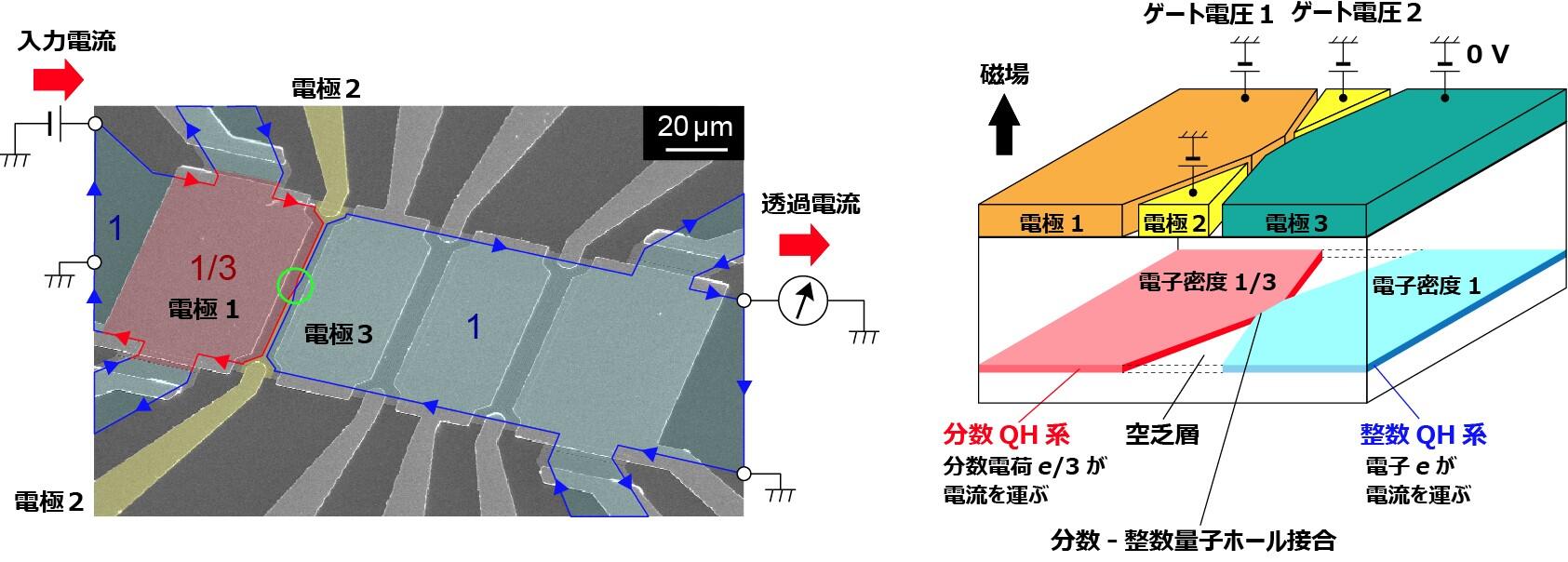図２：実験の概念図

左：試料の電子顕微鏡写真に色付けしたもの。赤色領域は電極１にゲート電圧１を印加して形成したランダウ準位占有率1/3の分数量子ホール（QH）領域、黄色領域は二次元電子系を狭窄するための電極２、青色領域はランダウ準位占有率1の整数量子ホール（QH）領域（電極３は0 Vに固定）。それ以外の濃いグレーの領域は半導体をエッチングして削った領域、薄いグレーの領域は本実験で使用しないゲート電極。緑色の円で囲った領域の中心部に微小な分数-整数量子ホール接合が形成される。量子ホール領域では試料の端のエッジチャネル（図中矢印）に沿って一方向に電流が流れるため、透過電流と反射電流をそれぞれ測定することができる。
右：分数-整数量子ホール接合（左図で緑色の円で囲った領域）の概念図。電極２にゲート電圧２を印加して直下の二次元電子系を空乏化すると、分数領域と整数領域が1 μm以下の幅で接触した接合を形成できる。接合の幅は、ゲート電圧２の負電圧が大きくなり空乏領域が広がるほど狭くなる。

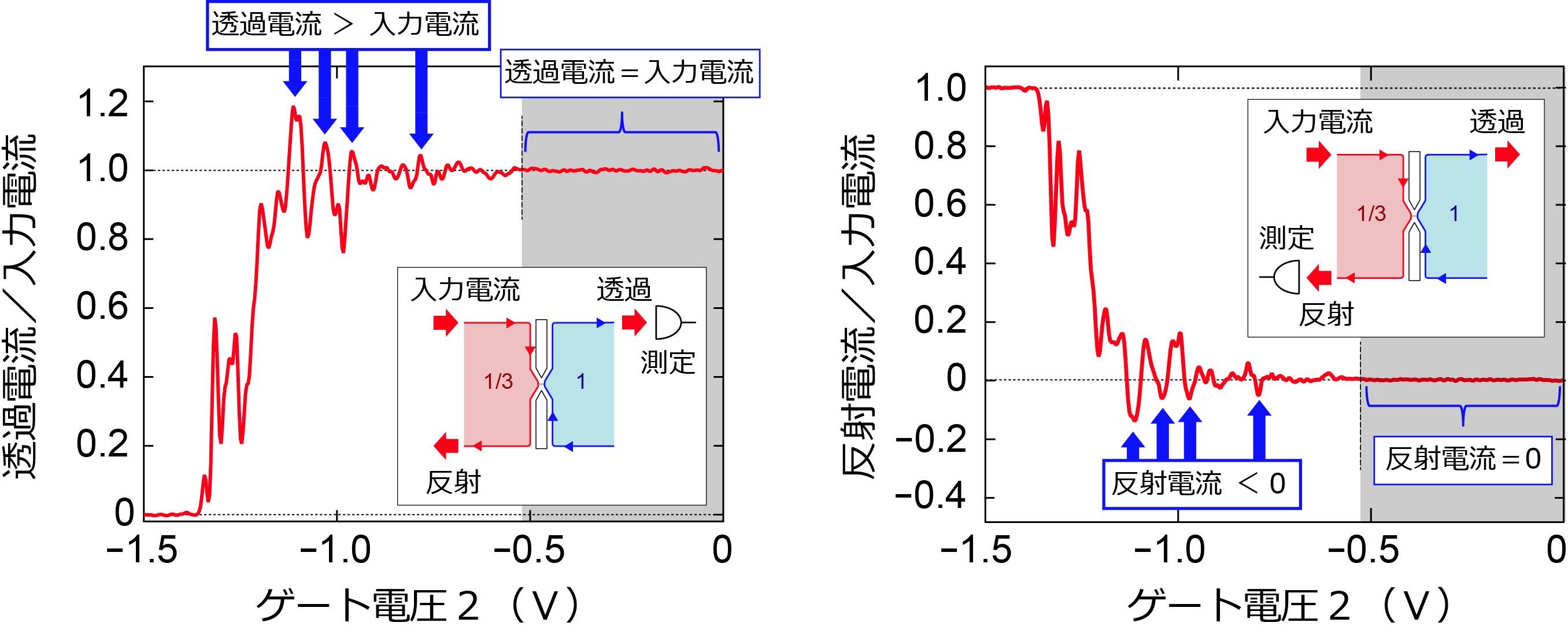図３：ゲート電圧２を印加して二次元電子系を狭窄したときの透過電流および反射電流の測定結果

左：透過電流の測定結果。微小接合が形成されていない領域（グレー領域）では入力電流と透過電流は等しいが、微小接合が形成されると（ゲート電圧２：-0.6 V以下）透過電流が振動し、入力した以上の電流が観測される場合がある（青矢印）。
右：反射電流の測定結果。実験では電圧を測定し、電流に換算してプロットし直した。透過電流の増大（左図）と同時に負の反射電流が観測される（青矢印）。
これら透過電流の増大、および負の反射電流がアンドレーエフ反射の証拠である。