公開鍵や暗号文サイズが小さく計算効率の高い同種写像暗号QFESTAを開発
～NIST標準化候補（SIKE）を破った攻撃手法を利用し新たな構成に成功～

発表のポイント：

1. 背景

量子計算機は量子力学の原理を応用した計算機で、現在世界中で開発競争が進められています。1994年に示されたShorのアルゴリズム（※4）により、現在広く使われているRSA暗号や楕円曲線暗号は量子計算機が実現すれば解読されてしまうことが判明しています。このため、量子計算機でも解読不可能な耐量子計算機暗号の研究が近年活発に行われています。
　耐量子計算機暗号の候補には、格子暗号、符号暗号、同種写像暗号などいくつかの種類があり、ポートフォリオ戦略として同時進行で研究が進められています。中でも、同種写像に基づく暗号方式である同種写像暗号は、ほかの候補と比べて公開鍵や暗号文のデータサイズが小さいことから注目されています。（図1：QFESTAと主要な耐量子暗号のデータサイズの比較）
　特に、同種写像に基づく暗号方式（カプセル化方式（※5））であるSIKEは、アメリカ国立標準技術局（NIST）の標準化コンペ（※6）でRound 4に残るなど注目を浴びていました。しかしながら、2022年にSIKEの安全性を破る攻撃手法（※7）が発見されたことで、この方式はもはや安全ではなくなりました。それ以降、多くの代替案が提示されてきましたが、いずれも暗号化と復号にかかる計算コストに大きな課題を抱えていました。この課題を解決するため、新たな同種写像暗号の開発が進められており競争が激化しています。

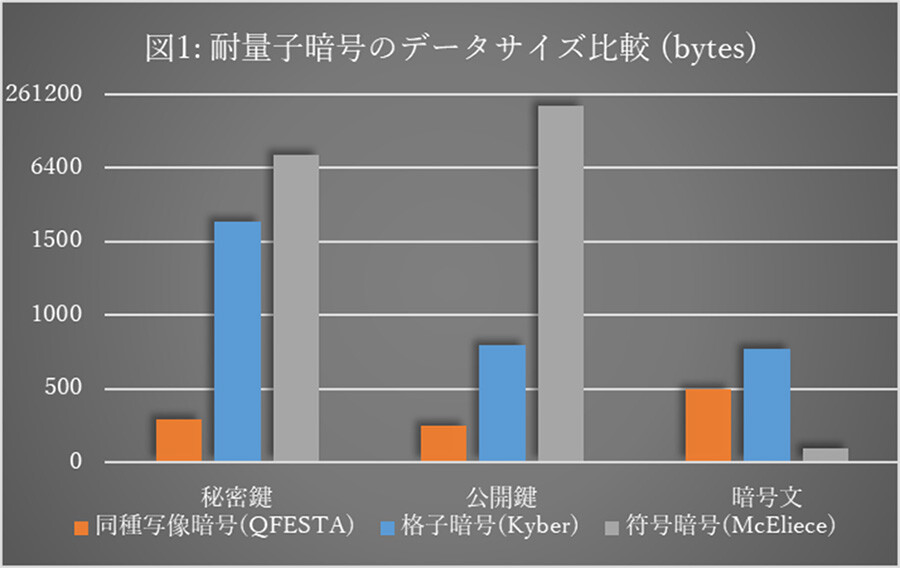秘密鍵：提案方式QFESTAは格子暗号（Kyber）と比較し1/5以下。符号暗号（McEliece）と比較し1/20以下。
公開鍵：提案方式QFESTAは格子暗号（Kyber）と比較1/3以下。符号暗号（McEliece）と比較し1/800以下。
暗号文：提案方式QFESTAと比較し符号暗号（McEliece）は1/5以下と小さいが、符号暗号（McEliece）は、秘密鍵や公開鍵のサイズが提案方式QFESTAと比較すると極めて大きい。

2. 研究の成果

NTTは、東京大学との共著論文（※8）において、SIKEに代わる新たな同種写像暗号であるQFESTAを開発しました。SIKEに対する攻撃手法を利用することで、RandIsogImagesと呼ばれる非滑らかな次数（※9）の同種写像を計算する新たなアルゴリズムを構成し、このアルゴリズムを応用することで、従来と比べて2倍以上高速な同種写像暗号QFESTAの構成に成功しました。安全性についても、いくつかの仮定の下でNISTが定める安全性レベル（※10）を満たすことを数学的に証明しました。
　今回提案したQFESTAは、SIKEの代替案として提案された数多くの方式の中で最も計算効率が高い方式です。（図2：従来手法との計算時間の比較を示します）また提案アルゴリズムRandIsogImagesは、次数に対する制約がほとんどないという点で汎用性の高いアルゴリズムであり、今後の同種写像暗号の開発を推進する構成要素になると期待されます。

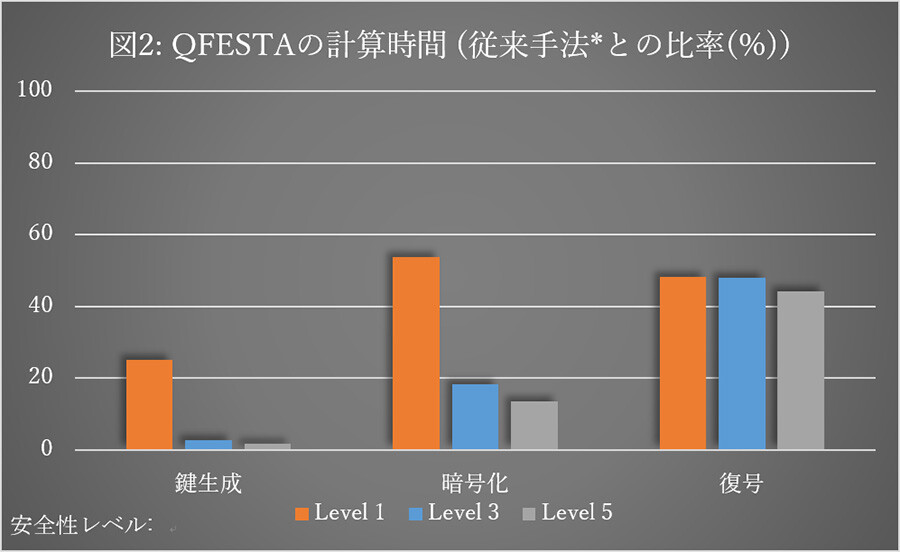安全性レベルが高いほど計算時間は大きくなる。
従来手法のFESTAのほうがQFESTAに比べその上昇率が大きいため、グラフに示した比率は減少している。
* FESTA: Fast Encryption from Supersingular Torsion Attacks. Andrea Basso, Luciano Maino, and Giacomo Pope. (2023)

3. 今後の展開

今後は提案アルゴリズムRandIsogImagesの電子署名等の暗号プロトコルへの応用についても検討を進め、電子署名等の耐量子化にも貢献します。
　また、本研究を通じ、量子計算機時代の到来に備えた、安心・安全な通信を提供する暗号プロトコルの開発により一層貢献して参ります。

【用語解説】

^（※1）同種写像：楕円曲線間の準同型写像の一種。二つの楕円曲線が与えられた際にその間をつなぐ同種写像を求めることは量子計算機を用いても困難であると考えられている。

^（※2）IND-CCA：選択暗号文攻撃に対する識別不可能性。暗号方式における最も高い安全性。

^（※3）CRYPTO 2024：https://crypto.iacr.org/2024/

^（※4）Shorのアルゴリズム：量子計算機により実行可能なアルゴリズム。このアルゴリズムを用いることで、素因数分解問題や離散対数問題といった数学的問題を通常の計算機よりも高速で解くことができる。Algorithms for Quantum Computation: Discrete Logarithms and Factoring. Peter W. Shor. (1994)

^（※5）カプセル化方式：鍵交換を行うための暗号方式の一種。

^（※6）NISTの標準化コンペ：Post-Quantum Cryptography | CSRC (nist.gov)

^（※7）An efficient key recovery attack on SIDH. Wouter Castryck, Thomas Decru. (2022)

^（※8）QFESTA: Efficient Algorithms and Parameters for FESTA using Quaternion Algebras. Kohei Nakagawa (NTT Social Informatics Laboratories), Hiroshi Onuki (The University of Tokyo). (2024)

^（※9）非滑らかな次数：同種写像には次数と呼ばれる概念があり、それが「滑らか」、すなわち小さな素因数のみからなる場合は従来手法により効率的に計算可能であったが、非滑らかな次数に対してはこれまで効率的に求めることは困難であった。

^（※10）NISTが定める安全性レベル：レベル1-5の安全性が存在し、数値が大きいほど安全性が高い。例えばレベル1はその暗号への攻撃にかかるコストが、共通鍵暗号AES-128への攻撃にかかるコストと同程度であることを意味し、レベル5は共通鍵暗号AES-256への攻撃にかかるコストと同程度であることを意味する。