追加情報を漏らさずに真実性保証ができる「ゼロ知識証明」における未解決問題を解決
～証明生成時に乱数を再利用しても秘密情報が漏れないゼロ知識アーギュメントの実現方針を確立～

発表のポイント：

1. 背景

ゼロ知識証明はある命題（主張）が正しいことを一切の追加情報を開示することなく証明する暗号プロトコルの一つです。例えば、パスワードを開示せずに正しいパスワードを持っていることを証明する認証技術として使用できるほか、個人情報を相手に提示することなく年齢確認が可能となるためプライバシー保護の観点からも画期的な技術です（図1）。近年では、暗号通貨において取引内容を秘匿したまま取引が正しく実行されたことを証明するためにも利用されており、注目されています。
　ゼロ知識証明の中で非常に安全性の高いものとしてリセット可能統計的ゼロ知識アーギュメントがあり、これは証拠暗号と呼ばれる暗号技術を用いることで実現できることが知られています。しかし、証拠暗号を使わずにリセット可能統計的ゼロ知識アーギュメントが実現できるかは未解決問題となっていました。

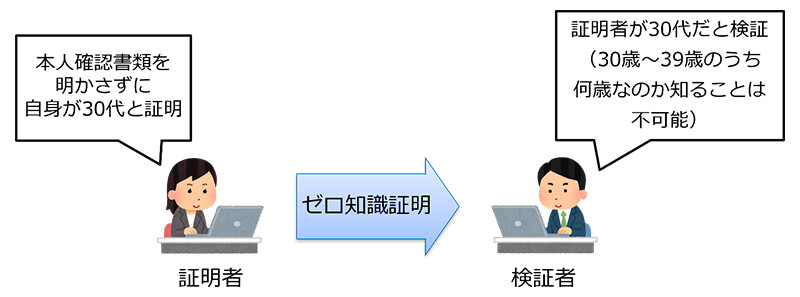図1：ゼロ知識証明による年齢確認の例

2. 本研究の成果および技術のポイント

今回、証拠暗号を使わずにリセット可能統計的ゼロ知識アーギュメントを実現することは不可能ということを証明し、上記の未解決問題を解決しました。特に、リセット可能統計的ゼロ知識アーギュメントを用いると証拠暗号を構築できることを示し、それによりリセット可能統計的ゼロ知識アーギュメントを実現することは証拠暗号を実現することと等価であることを示しました（図2）。
　技術的ポイントとして、本研究ではリセット可能統計的ゼロ知識アーギュメントの安全性を直接的に証拠暗号の実現に利用する代わりに、以下の2ステップによりリセット可能統計的ゼロ知識アーギュメントの安全性を間接的に利用することで証拠暗号を実現しました。

具体的には、まずリセット可能統計的ゼロ知識アーギュメントの高い安全性は証明者が送信するメッセージに大きな制約をかけることに着目し、ある特定の場合では証明者が送るメッセージが秘密情報に依存せず証明者が用いる乱数のみで定まらなければならないことを示しました。次に、この性質が比較的簡単に証拠暗号の実現へ利用できるものであることに着目し、それによりリセット可能統計的ゼロ知識アーギュメントから証拠暗号を実現しました（図3）。

図2：本研究の成果

図3：本研究の技術的ポイント

3．今後の展開

今後もゼロ知識証明の研究開発を推進し、IOWN PETsの一技術として、データが生成されてから消滅するまでの全ての期間において、データ所有者のポリシーの範囲内でのみ利用されることを技術的に保証し、安全なデータ流通を可能とする「平文のない世界」をめざすことに貢献して参ります。また、将来的にはNTTが研究するLLM tsuzumiのセキュアな学習への適用やNTTが推進するIOWN PETs機能として実用化することをめざします。

【用語解説】

^※1ゼロ知識証明（zero-knowledge proof）
ゼロ知識証明は証明者と検証者と呼ばれる二者の間で行われる暗号プロトコルです。大まかには、ゼロ知識証明では証明者による検証者に対する証明が以下の形で行われます。証明開始時には、証明者と検証者の両者は証明される命題を公開情報として持ち、更に証明者は命題が成り立つことの証拠を秘密情報として持っています。そして、検証者による質疑に証明者が回答するという質疑応答形式の対話を行うことにより証明者は命題が真であることの証明を行い、検証者は証明者による応答内容をチェックすることで証明を検証します。ゼロ知識証明が保証する安全性には、完全性（適切な証拠を持つ証明者が真の命題を証明できること）、健全性（悪意のある証明者が偽の命題を証明できないこと）、およびゼロ知識性（証明者の持つ証拠について命題の真偽以上の情報が悪意のある検証者に対して漏れないこと）の三つがあります。

^※2統計的ゼロ知識アーギュメント（statistical zero-knowledge argument）
ゼロ知識証明は、ゼロ知識性をどのような計算能力の攻撃者に対して保証するかに応じて計算量的（computational）と統計的（statistical）の二つに大別されるとともに、健全性をどのような計算能力の攻撃者に対して保証するかに応じて証明（proof）とアーギュメント（argument）の二つに大別されます。ゼロ知識性が無限の計算能力を持つ攻撃者に対して保証され、健全性が現実的な上限付きの計算能力を持つ攻撃者（具体的には多項式時間攻撃者と呼ばれるもの）に対してのみ保証される場合のゼロ知識証明を、統計的ゼロ知識アーギュメント（statistical zero-knowledge argument）と呼びます。

^※3リセット可能統計的ゼロ知識アーギュメント（resettable statistical zero-knowledge argument）
リセット可能統計的ゼロ知識アーギュメント（resettable statistical zero-knowledge argument）は、複数の証明が同じ乱数を用いて生成された場合でもゼロ知識性を保証する統計的ゼロ知識アーギュメントです。乱数の使用はゼロ知識証明を含む多くの暗号技術に不可欠であることが知られていますが、暗号技術に必要となる真の乱数の生成には物理現象の利用などが必要となるため生成コストが高いことが問題となります。リセット可能統計的ゼロ知識アーギュメントは乱数を再利用してもゼロ知識性を保証するため、真の乱数を事前に一度だけ生成しておけば証明生成時の乱数生成が不要になり、真の乱数の生成が難しい環境でも使用できるというメリットがあります。

^※4証拠暗号（witness encryption）
証拠暗号（witness encryption）は公開鍵暗号の一般化として提案された暗号技術です。通常の公開鍵暗号では公開鍵で暗号化を行い対応する秘密鍵で復号を行いますが、証拠暗号では任意のNPインスタンス（NP instance、問題例［例えば数学の定理など］）を用いて暗号化を行い対応する証拠（witness、問題例に対する効率的に検証可能な答え［例えば定理に対する証明など］）を用いて復号を行います。

^※5IOWN PETs： https://www.rd.ntt/sil/project/iown-pets/iown-pets.html