「二分決定グラフ」の演算にかかる最悪時間計算量を証明
～計算機科学分野の数十年来の未解決問題を解決～

発表のポイント：

1. 背景

二分決定グラフは集合族を表現するデータ構造です。集合族とは、集合を要素とするような集合のことです。例えば集合族｛｛1, 2｝,｛2, 3｝｝は、集合｛1, 2｝, 集合｛2, 3｝からなる集合族です。論理回路やある地点から別の地点までの移動経路の組合せ、同時に利用可能なクーポンの組合せなど、様々な対象が集合族として表現することができます。集合族の汎用性と、それを表現するデータ構造としての利便性から、回路設計や通信ネットワークの解析、AIなどの集合族を扱う多様な課題において二分決定グラフが利用されてきました。例えば、通信ネットワークの解析において、複数地点が接続されるネットワークの通信パターンを集合族で表現し、さらに二分決定グラフで表現することにより、解析にかかる時間を大幅に削減できることがわかっています（図1）（※4）。

図1： ネットワークの通信パターンを表現する集合族、二分決定グラフの例。図では16個の通信パターンを16個の集合からなる集合族で表現し、それを11個のノード（節点）を結ぶ線からなる二分決定グラフに圧縮して表現している。
（左）4個の点をつなぐネットワークの模式図と16の通信パターンの例
（中）通信パターンを各辺の番号を要素とする集合の集合族で表現したもの
（右）各要素が集合族中の集合に含まれている/いないの決定をノードとして持つような二分決定グラフ。集合族中のすべての集合は、最上段からノードを経由しながら最下段のTまで下向きにたどる経路として表現される。ある集合に対応する経路において、あるノードから出る線が実線ならば対応する要素がその集合に含まれることを表し、点線ならば含まれないことを表す。図中青字の経路は、1から実線で2へ、2から点線で3へ、...、5から実線で最下段Tへ進むことから、集合｛1, 4, 5｝が集合族に含まれていることがわかる。

二分決定グラフの重要な特徴として、ある集合族を表現する二分決定グラフに、演算とよばれる各種操作を適用することによって、別の集合族を表現する二分決定グラフを効率的に構築できるという点が挙げられます。例えば二つの二分決定グラフに対して、それらが表す集合族の和集合（Union）や、集合族の積（Join）を表現する二分決定グラフを効率的に構築することができます（図2）。これらの演算を活用することで、例えば経路の集合から移動距離が一定以下のものを取り出すなど、集合族に対するさまざまな操作を柔軟に実行することができます。二分決定グラフの研究分野ではこれまでに多様な演算が考案されて利用されてきました。

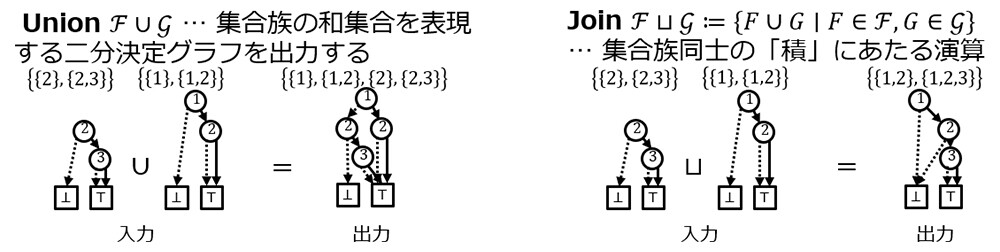図2： 二分決定グラフに関する二項演算の例。集合族を表す二つの二分決定グラフを入力として受け取り、それらに演算を実行した結果を表す二分決定グラフを出力する。

しかしながら、二分決定グラフに関する演算に、最悪の場合どれくらい時間がかかり得るのかは、基本的な演算を除く多くの演算に対しては知られていませんでした。さらに、また、一部の演算については著名な教科書に多項式時間で実行可能であると記載されているものの、多項式時間で実行可能であることに関する証明が存在しませんでした。

2. 成果の内容

本研究では、計算量が未知であった、二分決定グラフの主要な演算群に対して、最悪の場合に入力サイズに対して実行に指数時間かかる可能性があることを初めて理論的に示しました。具体的には、集合の要素数nが与えられたときに、入力の二分決定グラフのサイズがnに対する多項式に比例するが、出力のサイズがnに対して指数的に増大するような事例を演算ごとに示すことで最悪時の計算量を示しました。演算によっては、広く利用されてはいるものの、考案されて以来数十年間計算量が未知であるものも存在することから、本研究は二分決定グラフに関する数十年来の未解決問題を解決したといえます。

3. 技術のポイント

二分決定グラフの基本的な演算である、共通部分（Intersection）・和集合（Union）演算を複数回繰り返すと、決定グラフのサイズが指数的に増加することが以前より知られていました。今回、集合族の積（Join）に代表される計算量が不明だった演算について、一度の演算の実行が複数回の共通部分・和集合演算と等価となり得ることを発見しました。この発見をもとに、一度の演算によって二分決定グラフのサイズが指数的に増加する事例を示すことによって、多項式時間で演算を実行することが不可能であることを証明しました（図3）。

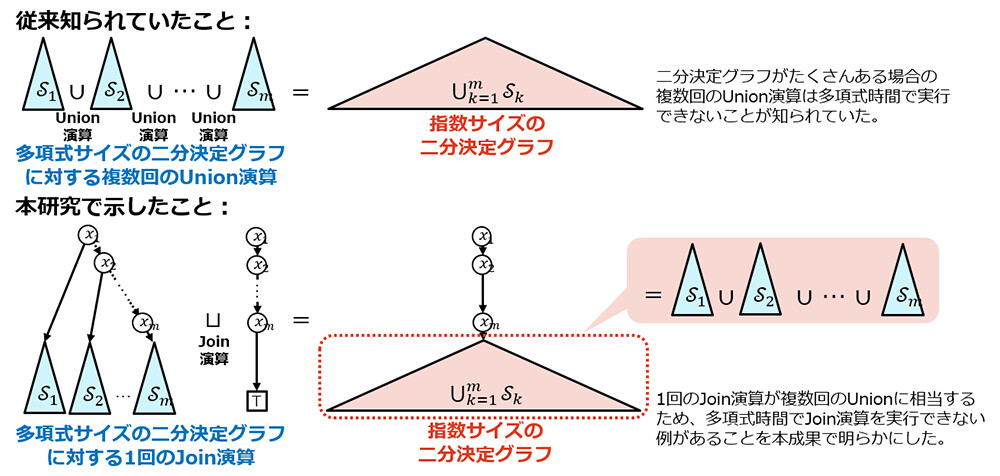図3： 二分決定グラフのJoin演算が多項式時間で実行不可能であることの証明のポイント

4. 研究の意義・今後の展開

本研究成果により、二分決定グラフに関する主要な演算すべてについてその最悪時の計算時間が明らかになりました。この結果は広く用いられているデータ構造である二分決定グラフを用いた問題解決法に適用できる、非常に影響範囲の広い理論的な成果です。計算量を明らかにすることで、計算量の指数的な増加を防ぐために特定の演算の利用を避けるといった意思決定が可能となるため、ネットワーク設計や道路などのインフラ整備の場面などにおいて、より効率的なアルゴリズムの設計に貢献が期待できます。また、計算機科学に関する著名な教科書であるTAOCPには、本成果によって指数時間かかることが示された一部の演算が、多項式時間で計算可能であるという記述がありました。本成果はこの記述の誤りを指摘するものであり、研究チームからの修正案は著者のDonald Knuth博士に承諾され、TAOCPに反映される予定です。

【論文情報】

会議名： 35th International Symposium on Algorithms and Computation（ISAAC 2024）
題 名： Single Family Algebra Operation on BDDs and ZDDs Leads to Exponential Blow-Up
著者名： Kengo Nakamura, Masaaki Nishino, and Shuhei Denzumi
DOI： 10.4230/LIPIcs.ISAAC.2024.52
URL： https://doi.org/10.4230/LIPIcs.ISAAC.2024.52

【研究助成】

本研究は、JST CREST（課題番号：JPMJCR22D3）、科研費（課題番号：JP20H05963、JP23H04391）の助成により実施されました。

【用語解説】

^※1集合族：集合をあつめた集合のこと。例えば｛｛1, 2｝,｛2, 3｝｝は、数字の組み合わせである集合｛1, 2｝,｛2, 3｝を集めて構成される集合族である。ネットワーク解析の例では、ネットワーク上の2つの拠点間を結ぶ接続経路をリンクの集合として表現することで、複数の接続経路を集めたものを集合族として表現できる。

^※2指数時間アルゴリズム：解くべき問題の入力のサイズをnとしたときに、アルゴリズムの実行にかかる時間が指数関数的に増大するアルゴリズムのこと。

^※3多項式時間アルゴリズム：解くべき問題の入力のサイズをnとしたときに、アルゴリズムの実行にかかる時間の上限がnの多項式で表現できるアルゴリズムのこと。

^※4規模の大きな解析についての解析はこちらを参照。
https://www.rd.ntt/research/JN202409_29259.html