世界初、量子超越性と暗号の安全性が等価であることを証明
--従来とは異なるアプローチによる量子計算機の優位性を特徴付ける新たな理論的基盤--

概要

白川雄貴 基礎物理学研究所博士課程学生、森前智行 同准教授、山川高志 NTT社会情報研究所上席特別研究員（兼：基礎物理学研究所特任准教授）の研究グループは、量子計算機が古典計算機よりも高速であることの必要十分条件を暗号理論の観点から明らかにしました。量子計算機は古典計算機を凌駕する計算能力が期待されていますが、この量子超越性¹が存在するためには何が必要なのか、その条件はこれまで明確にされていませんでした。本研究は量子超越性と暗号の安全性が等価であることを証明し、量子超越性の必要十分条件に対して初めて明確な解答を与えました。さらに興味深いことにこの成果は、量子超越性が存在しない場合、現在安全とされている暗号機能の多くが破られることも意味します。これは、情報セキュリティ分野にとっても重要な意味を持ち、量子超越性の存在そのものが暗号の基盤と密接に結びついていることを示しています。
　本研究成果は、2025年6月27日に国際会議「57th Annual ACM Symposium on Theory of Computing（STOC 2025）」にて発表され、国際学術誌「Proceedings of the 57th Annual ACM Symposium on Theory of Computing」にオンライン掲載されます。

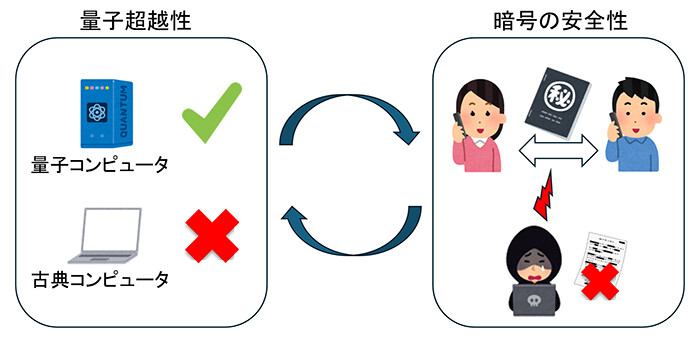図1：本研究では特定のタスクにおける量子超越性（左）の存在を証明するために暗号の安全性（右）を仮定することが必要十分であることを明らかにしました。

1. 背景

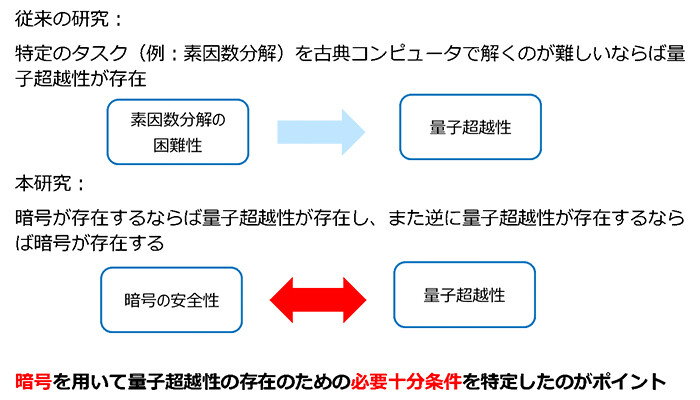
量子計算機は、量子力学の基本原理である重ね合わせの性質をうまく活用することで計算を行う革新的な技術です。これにより、古典計算機では膨大な計算時間を要すると考えられる困難な問題を高速に解く可能性が期待されています。ところが、そのような量子超越性は常に存在するとは限りません。したがって、量子計算機の性能を正しく理解し、その能力を活かすためには、「どのような条件の下で量子超越性が存在するのか」、「量子超越性が存在するために何が必要か」といった問いへの明確な答えが不可欠です。これまでにも、例えば素因数分解の困難性などさまざまな条件が提示され、その条件のもとで量子超越性の存在が証明されてきました。しかし、それらはあくまで十分条件であり、それらの条件が本当に必要なのかについては明確に理解されてはいませんでした。
　そこで、本研究では量子超越性の理論的な土台をより強固なものとするために、「量子超越性の必要十分条件は何か？」という根本的な問題に取り組みました。

2. 研究手法・成果

今回、量子超越性の必要十分条件を特定することに初めて成功しました。特に、近年量子暗号²の分野で提案されているある種の暗号機能の安全性と量子超越性の存在が等価であることを示しました。この等価性とは、暗号機能が安全であれば量子超越性を示すタスクを構成することができ、量子超越性が存在するならば安全な暗号機能が構成できる、という意味です。
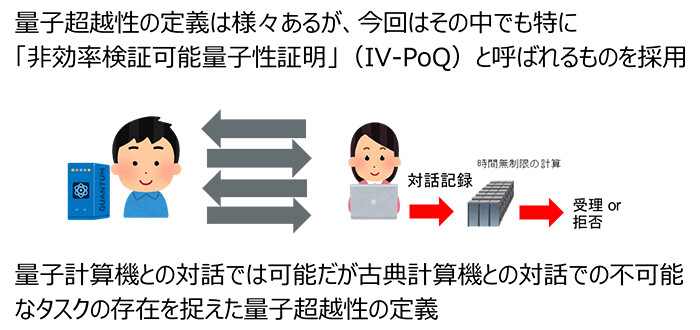
　この成果は、量子計算理論と暗号理論でそれぞれ発展してきたテクニックや考え方を統合し、「量子超越性」と「暗号の安全性」という一見関係のなさそうな2つの概念を結びつける新しい枠組みを提案することで実現されました。特に本研究では「非効率検証可能量子性証明（IV-PoQ：Inefficient-Verifier Proofs of Quantumness）」と呼ばれる対話型プロトコルに着目しました。これは、量子計算機を持たない検証者が、量子計算機を持つ証明者とやりとりをすることで、相手が本当に量子計算能力を持っているかを検証できる仕組みです。このプロトコルが存在するための必要十分条件がある種の暗号機能の安全性に一致することを数学的に証明し、量子超越性と暗号の安全性が等価であることを示しました。

3. 波及効果、今後の予定

本研究成果の意義は、量子超越性と暗号の安全性が等価であることを証明し、量子超越性の必要十分条件を明らかにしたことにあります。量子計算理論と暗号理論の間に存在するこの密接な関係により、両分野において以下のような相互的な影響が期待されます。まず、将来的な量子超越性の実証実験やさらなる理論研究が暗号理論的により強固な基盤のもとで進められることが見込まれます。さらに興味深いのは、今回の成果が「もし量子超越性が存在しないのであれば、現在安全とされている多くの暗号機能の安全性が破綻してしまう」ことをも意味している点です。特筆すべきは、ここで安全性が破綻する暗号機能は量子暗号だけではなく、今日広く利用されている古典計算機上の暗号や今後の普及が急がれている耐量子計算機暗号も含む点です。これは、情報セキュリティ分野にとっても非常に重要な示唆であり、量子計算機の優位性と暗号理論の基盤が深く関係していることを明らかにしています。そのため本研究成果は、量子計算機実現後にも安全に使用できる暗号の構成に向けた基盤理論への貢献も期待されます。

このように本研究は暗号理論に基づいた量子超越性研究の新たな応用を切り拓く可能性を示しました。

4. 研究プロジェクトについて

本研究はJST CREST JPMJCR23I3、JST Moonshot R&D JPMJMS2061-5-1-1、JST FOREST、MEXT QLEAP、the Grant-in Aid for Transformative Research Areas（A）21H05183、the Grant-in-Aid for Scientific Research（A）No.22H00522、JST SPRING JPMJSP2110の支援を受けて行われました。

＜用語解説＞

＜研究者のコメント＞

「本研究では、量子超越性の必要十分条件を暗号理論的観点から特徴づけることに成功しました。証明のテクニックは暗号理論的なアイデアと量子計算のアイデアをうまく組み合わせたものであり、個人的には面白い手法を提案できたと思っています。今後は、さらに広範な量子超越性の特徴づけを目指していきたいです。」（白川雄貴）

＜論文タイトルと著者＞

タイトル：Cryptographic Characterization of Quantum Advantage（量子超越性の暗号理論的特徴付け）
著者：Tomoyuki Morimae, Yuki Shirakawa, Takashi Yamakawa
掲載誌：Proceedings of the 57th Annual ACM Symposium on Theory of Computing
DOI：10.1145/3717823.3718133