量子計算機が古典計算機よりも高速に解けることを示す新たなアルゴリズムを世界で初めて考案
～周期性のような「構造」を持たない関数を用いた問題で検証可能な優位性を示す～

日本電信電話株式会社（本社：東京都千代田区、代表取締役社長：島田　明、以下「NTT」）は、出力が周期性のような「構造」を持たない関数を用いた問題に対し、検証可能な量子計算機の優位性（量子優位性）を示す新たな量子アルゴリズムを世界で初めて考案しました。これは、Shorの素因数分解アルゴリズム(1994年)以来、約30年ぶりの本質的に新しいアイディアに基づく、検証可能な量子優位性を示すアルゴリズムの提案です。本成果により、これまで実用的な量子アルゴリズムを見つけることは難しいと考えられてきた問題に対するアルゴリズムの研究が促進され、将来の量子計算機の適用範囲が広がることが期待されます。
　なお、本成果は理論計算機科学における最高峰の国際会議であるIEEE Symposium on Foundations of Computer Science (FOCS) 2022（※1）において発表されます。

1．背景

量子計算機は量子力学の特性を利用した計算機で、量子化学計算やある種のシミュレーションなど、既存の古典計算機では計算時間が爆発的に増加し解くことが困難である問題を高速に解くことができると期待されており、世界中で熾烈な研究開発競争が行われています。また、計算機科学の理論面からも、どのような問題であれば量子優位性、すなわち量子計算機が古典計算機よりも高速に解けることが示されるのか、研究が進められています。
　量子計算機が高速に解ける問題として、1994年に示されたShorの素因数分解アルゴリズムがよく知られています。しかし、どのような問題であれば量子計算機で高速に解けるのかという点については、未解明な点も多くあります。

2．研究の成果

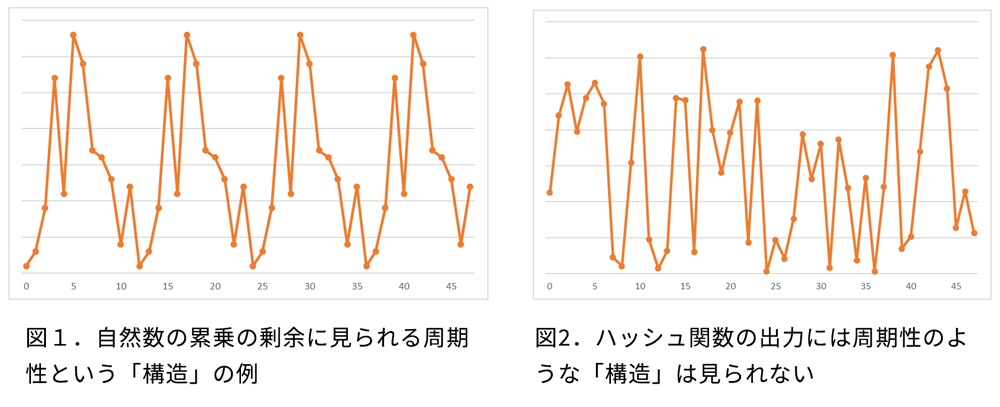
Shorの素因数分解アルゴリズムは、自然数の累乗の剰余が周期性という「構造」を持っていることを利用したアルゴリズムです（図1）。一方でハッシュ関数（※2）の出力には、周期性のような「構造」はありません（図2）。ハッシュ関数のような「構造」を持たない関数を用いた問題について、検証可能な量子優位性を示す結果はこれまで知られていませんでした。NTTの山川高志特別研究員は、NTT Research Cryptography & Information Security LabのMark Zandry博士と共著で投稿した論文（※3）において、「構造」を持たない関数のみを用いた問題に対し、検証可能な量子優位性を示す量子アルゴリズムを世界で初めて示しました。山川らは、構造を持たないランダムな関数（入力nビット、出力1ビット）の出力が0になる入力を見つけるという問題に、その入力が誤り訂正符号(※4)にもなっているという条件を加えることで、量子計算機では高速に解けるが、古典計算機では高速に解の探索ができないという問題を定義することに成功しました。この「構造」を持たない問題に対する検証可能な量子優位性を示す量子アルゴリズムの発見により、これまで量子計算機による高速なアルゴリズムが知られていなかった種類の問題に対しても、高速な量子アルゴリズムが発見されることが期待され、将来の量子計算機の適用範囲を広げうる、ブレークスルーといえる研究成果です。

本成果はarXiv（※5）に公開された時から注目を集めており、山川らへのインタビュー取材をもとに、サイエンス分野の著名なウェブサイトであるQuanta Magazineへの記事掲載もされました（※6）。
　また、本成果は理論計算機科学における最高峰の国際会議であるIEEE Symposium on Foundations of Computer Science (FOCS) 2022に採択され、10/31のSession 1Bにおいて発表される予定です。なお、山川特別研究員の論文がFOCSに採択されるのは、昨年度（※7）に続き2年連続の快挙となります。

^（※1）FOCS 2022 https://focs2022.eecs.berkeley.edu/index.html

^（※2）ハッシュ関数：任意のデータから、別の短い値を得る関数。電子署名などに使われる。SHA-1やその後継であるSHA-2が有名。

^（※3）Verifiable Quantum Advantage without Structure. Takashi Yamakawa (NTT Social Informatics Laboratories), Mark Zhandry (Princeton University and NTT Research).

^（※4）誤り訂正符号：データの記録や伝送の際に誤りが発生しても元の正しい符号を復元できる特徴を持つ符号。リード・ソロモン符号などが有名。

^（※5）https://arxiv.org/abs/2204.02063

^（※6）Quantum Algorithms Conquer a New Kind of Problem
https://www.quantamagazine.org/quantum-algorithms-conquer-a-new-kind-of-problem-20220711/

^（※7）理論計算機科学における世界最高峰の国際会議FOCSに採択
https://group.ntt/jp/topics/2022/02/08/accepted_paper_focs2021.html